1 Introduction

Two things juxtaposed for this post. The first was learning from Niles Johnson of a way to generate Pythagorean triples using lines and circles. The second was learning that there are $320$ concepts to learn in order to take GCSE Mathematics.

One thing in the post about Pythagorean triples was the occurrence of the formulae:

$$x=\frac{1-t^2}{1+t^2},y=\frac{2t}{1+t^2}.$$

Now, it might just be the generation that I am, but I remember learning those formulae at school as how to write cosine and sine in terms of the tangent of the half angle. The formula book1 even made the substitution $t=\tan (x/2)$ so that the formulae read:

$$\cos (x)=\frac{1-t^2}{1+t^2},\sin (x)=\frac{2t}{1+t^2}.$$

So when reading that post, I wondered if there were some way to exploit that relationship to simplify the argument.

I had a go at it, and found what I believe is such a simplification.

In doing that, I realised that yet again similar triangles are the key. Which brings me to those $320$ concepts. How many of them, I wonder, are just "similar triangles" dressed up in strange language?

2 Pythagorean Triples

Let's go through the first part of the search for Pythagorean triples. A Pythagorean triple, let's recall, is a set of three integers, say $a$, $b$, and $c$, which satisfy Pythagoras' theorem:

$$a^2+b^2=c^2.$$

This means that there is a right-angled triangle with integer sides.

Dividing through by $c^2$ yields:

$$\frac{a^2}{c^2}+\frac{b^2}{c^2}=1$$

and this means that $(\frac{a}{c},\frac{b}{c})$ are the coordinates of a point on the unit circle with the property that both coordinates are rational numbers.

Conversely, if $(x,y)$ is a point on the unit circle with both $x$ and $y$ rational, then we can put them over a common denominator and so write $x=\frac{a}{c}$ and $y=\frac{b}{c}$, then as they are on the unit circle we have $x^2+y^2=1$ which untangles to $a^2+b^2=c^2$.

So Pythagorean triples almost correspond to rational points on the unit circle. The "almost" is because if we multiply each number in a Pythagorean triple by the same constant then we get a new triple but they both give the same point on the unit circle. For example, $3,4,5$ and $6,8,10$ are different Pythagorean triples but $(3/5,4/5)$ and $(6/10,8/10)$ are the same point. We'll not bother about this.

In Niles Johnson's post, a diagram like Figure 1 appears.

In this, we can see the source of the half angle. The "angle at circumference is half angle at centre" rule leads to the conclusion that $P\hat{A}O$ is half of $P\hat{O}B$. So we could use some trigonometry to figure out the coordinates of $P$ in terms of the tangent of the angle at $P\hat{A}O$, and once we had that we would have the formulae from Niles Johnson's post.

3 Similar Triangles

But trigonometry is just another name for similar triangles. So is there a way to use similar triangles directly?

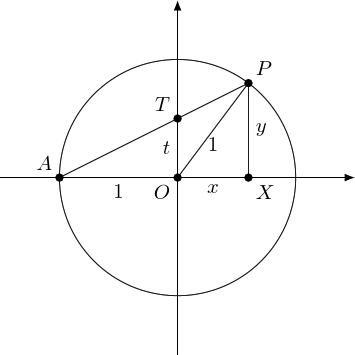
The tangent of the angle at $P\hat{A}O$ is the gradient of the line $AP$. Let's call this $t$. This is the height that the line rises for every one unit we go across. As we go across one unit from $A$ to $O$, the line $AP$ must cross the $y$–axis at height $t$. So we can also think of $t$ as the $y$–intercept of $AP$.

Our goal is the coordinates of $P$. It's a common thing to do to draw a right-angled triangle to illustrate the coordinates of a point, so let's adorn our diagram with that triangle. Adding both of these new features, we end up with Figure 2.

There are two obvious similar triangles here: $ATO$ and $APX$. We could exploit this similarity together with the fact that $(x,y)$ lies on the circle to find the formulae for $x$ and $y$. Pythagoras tells us that $x^2+y^2=1$, while similarity says that $y=t(x+1)$. But then we need to substitute in and solve, which leads to a quadratic. This is Niles Johnson's approach.

We can do better.

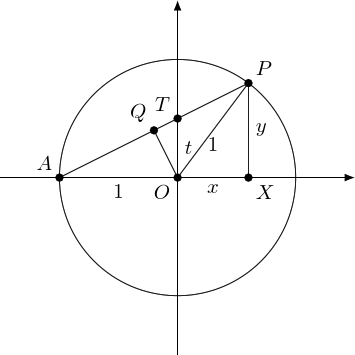
There's another similar triangle. Let's "drop" the perpendicular from $O$ to $AP$. As triangle $AOP$ is isosceles (since $AO=1=OP$), this bisects $AP$. Figure 3 is the result.

Now $O\hat{Q}A$ is a right-angle and so triangle $AQO$ is similar to $AOT$. What's a bit confusing here is that the triangles have been flipped, so the hypotenuse of $AQO$ is the base of $AOT$. Similarity then says:

$$\frac{AQ}{AO}=\frac{AO}{AT}.$$

As $AQ$ bisects $AP$, and using $AO=1$, this means that:

$$AP=\frac{2}{AT}.$$

Similarity also tells us that:

$$\frac{XP}{AP}=\frac{OT}{AT}.$$

Substituting in $y=XP$ and $t=OT$, we get:

$$\frac{y}{AP}=\frac{t}{AT}.$$

Putting these together yields:

$$y=t\frac{AP}{AT}=\frac{2t}{A{T}^2}.$$

Finally, $AT$ is the hypotenuse of the right-angled triangle $AOT$ so $A{T}^2=1^2+t^2$ and we get:

$$y=\frac{2t}{1+t^2}.$$

And using similarity again tells us that $y=t(1+x)$ which leads to:

$$t(1+x)=\frac{2t}{1+t^2}$$

and this rearranges to:

$$x=\frac{2}{1+t^2}-1=\frac{2-(1+t^2)}{1+t^2}=\frac{1-t^2}{1+t^2}.$$

4 Rational Points

The purpose of this is that if $t\in \mathbb{Q}$ then so also are $\frac{2t}{1+t^2}$ and $\frac{1-t^2}{1+t^2}$, meaning that the point $P$ has rational coordinates and we get a Pythagorean triple.

In fact, if we write $t=\frac{p}{q}$, then

$$x=\frac{1-\frac{p^2}{q^2}}{1+\frac{p^2}{q^2}}=\frac{q^2-p^2}{q^2+p^2},$$

and

$$y=\frac{2\frac{p}{q}}{1+\frac{p^2}{q^2}}=\frac{2pq}{q^2+p^2}.$$

This fits our pattern with $a=q^2-p^2$, $b=2pq$, and $c=q^2+p^2$, and thus this is our Pythagorean triple.

A bonus from this approach is that it shows that points in the unit circle with rational coordinates are dense. Pick a point $R$ on the circle with coordinates $(u,v)$. Then join $R$ to $A$. The slope of this line is $\frac{v}{1+u}$. Now choose $t$ to be a rational approximation to $\frac{v}{1+u}$. Then the resulting point $(x,y)$ is a rational approximation to $(u,v)$ lying on the unit circle.

And all from similar triangles!