1 Introduction

Two puzzles recently flew past me on social media, and something about them caught my attention long enough for me to try to solve them. The puzzles themselves are not particularly special, but I was in a reflective frame of mind so was aware of the process I went through when solving each and a few things clicked into place about puzzles and mathematics that I thought worth recording.

I should start by saying that I enjoy doing puzzles but I don't regard them as being related to real mathematics in any significant way. That may have something to do with the fact that I don't regard myself as being particularly good at them1 and there's always a temptation when one feels one isn't good at something to regard it as not really a serious pursuit.

So I'll happily work through some puzzles from time to time, but to my mind there's a qualitative distinction between solving puzzles and doing mathematics. It's a distinction that is important to make because many children are introduced to "real" mathematics via puzzles2 but find them not to their taste. Sadly, they then feel that mathematics is not for them. Not only is there far more to mathematics as a subject than is covered by such puzzles, but also the techniques and mind sets used for puzzle solving are not a fair reflection of those used in real mathematics.

2 The First Puzzle: A Question of Marriage

With both puzzles, it wasn't the actual puzzle that caught my attention but a comment by whoever set it. And in both cases, the comment was a goad rather than an inspiration. The first puzzle came with the words "I bet 80% of you will get this wrong!". Normally, that's enough to make me skip the puzzle altogether.

Rephrasing (because I can't be bothered to track down the original), the puzzle was:

Alice, who is married, is looking at Bob. Bob is looking at Charlie, who is unmarried. Is someone married looking at someone unmarried?

To cut to the chase, I got it wrong. The puzzle was set as a poll so I could put in my answer and get instant feedback in the form of telling me that my answer was incorrect and saying what the right answer was – but not why that was the right answer. What's interesting, to me, is how my thoughts then went. The first thing was that I instantly saw what I'd overlooked and so why the right answer was the right answer. The second thing was that I started trying to pick apart the question and see if there were some way of interpreting it so that my answer was right3.

But here's the rub. In the end, I understood the problem, figured out how it works, saw how it connects to other areas of mathematics, but ultimately felt like I'd failed. That comment, "I bet 80% of you will get this wrong!", meant that my initial failure still rankles. It still feels as though I failed.

3 The Second Puzzle: A Point of View

The second question also had an irritating comment. This one was "99% insight, 1% math". Quite apart from the "math", this showed a complete misunderstanding of what mathematics is about. What they meant by "math" was "arithmetic".

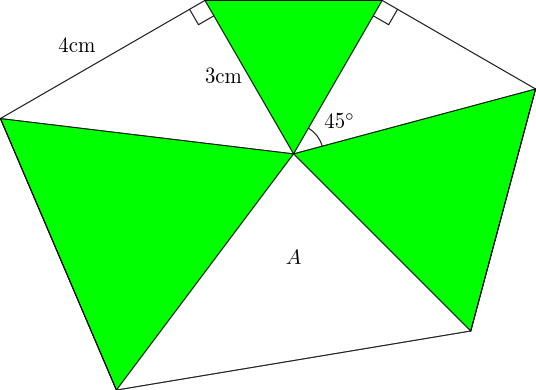
Anyway, the puzzle is in Figure 1.

The accompanying comment implied that there was some "insight" (aka trick) in solving this. So rather than simply calculate the area, I looked for some way to "see" what it should be. As per usual in this type of question, the first stage is to fill in any obvious missing information. The $3$–$4$–$5$ triangle is fairly trivial to spot, so the left-hand equilateral triangle has sides length $5cm$, meaning that one of the sides of the $A$ triangle is $5cm$. The ${45}^{\circ }$ angle in the other right-angle triangle means that the right-hand equilateral triangle has sides length $3\sqrt{2}cm$. So the triangle we're interested in has two sides of $5cm$ and $3\sqrt{2}cm$. We could work out the angle at the centre, although it's not going to be a "nice" angle since the angle in a $3$–$4$–$5$ triangle is not "nice", but if we were going to use it to work out the area of the triangle we'd only be interested in its sine anyway.

But using the sine formula for the area of a triangle seems to fly in the face of the "99% insight, 1% math" comment. So we're obviously meant to find a more cunning route to its area.

I'm not sure whether it is the colours or something else, but I soon hit on the idea of allowing the triangles to pivot at the centre and bring the white triangles together.

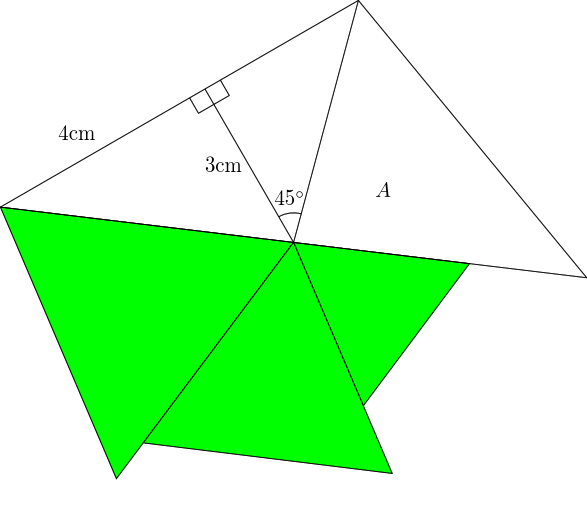
The result of this is in Figure 2. The only piece of missing information in this diagram which was (implicitly) in the first diagram is that the lower edge of the $A$ triangle is the same length as the hypotenuse of the left-hand right-angle triangle.

The first thing to spot is that the white region is, as it appears to be, a triangle. The two right-angles make the left-hand edge straight, and the three equilateral triangles make the lower edge straight.

At this point, common sense took over. Rather than look for further insight, I decided that the easiest thing would be to calculate the area almost directly. I say "almost" because although it is now possible to calculate the area directly, I didn't do that. Not because I couldn't, but because I didn't think to. What I decided to do, somewhat oddly4, was to calculate the area of the whole triangle and take away the area of the left-hand part.

A quick argument using similar triangles gives us the height of the full triangle as being $\frac{21}{5}cm$ and the base is $10cm$, so the area is $21{cm}^2$. The left-hand part (comprising both of the left-hand triangles) has "base" $7cm$ and "height" $3cm$ so has area $\frac{21}{2}{cm}^2$. This leaves:

$$21-\frac{21}{2}=\frac{21}{2}{cm}^2$$

for area $A$.

At this point I've solved the puzzle. I've found the area of $A$, and I think I've used a fair amount of insight and not too much arithmetic (still 100% maths, though). So I could leave it there. But I didn't. Because of my slightly odd last step, I found that the area of $A$ was half of the total area of the full triangle. This looked too much of a coincidence to me. I wanted to know if there was a particular reason for that: what was it about the set-up which gave $A$ the same area as the other two triangles combined?

It didn't take me long to realise that it was because the line that divides $A$ from the other half bisects the base of the triangle. So the two halves of the triangle have the same base and the same height and therefore the same area. Thus the area of $A$ is the same as the area of the other half, which is easily computed as $\frac{1}{2}\times 3\times 7{cm}^2$.

4 Solving Mathematically

I think I solved this second problem as a mathematician rather than as a puzzler. My steps were:

1. Look for ways to simplify the problem.

2. Don't shirk from doing an actual calculation.

3. Review the argument to see if there are any shortcuts in hindsight.

The first two steps in the above are focussed on the problem at hand. They are motivated by the desire to solve the problem, but with the proviso that the solution is the key. Neatness and beauty and elegance can wait, what matters most is the solution.

But once the problem has been solved, a mathematician doesn't put it on the shelf. The classic tales about "reducing to a problem that's already been solved" miss the point (deliberately, of course). We are continually revisiting problems, looking for ways to simplify their solution or to do more with them. Almost as if we had a new tool in our toolbox and were trying out different ways of using it to see what it was good for. Or, to use another analogy, we've put a new slab down and we're looking to see what we can build on it by testing it out, jumping up and down on it, and seeing if we can tip it over.

And that's the rationale behind the third step, the review. Once the solution is found, we look for insights and techniques that might be useful in solving other problems. This is what allows us to add to our toolbox. Without it, we gain nothing extra from solving the problem. With it, we gain a whole new strategy for solving other problems.

This, then, is my distinction between "recreational mathematics" and "real mathematics"5. What do you do when you've solved a problem? Do you say "Right, that's done. Time to do something else?". Or do you keep returning to it, examining it, turning it over in your mind, looking for more insights, more techniques, more stuff to do.

Proverbs 26v11 really ought to have read:

As a dog returns to its vomit, so mathematicians return to their mathematics.