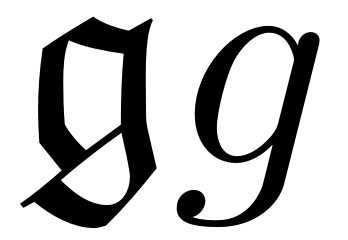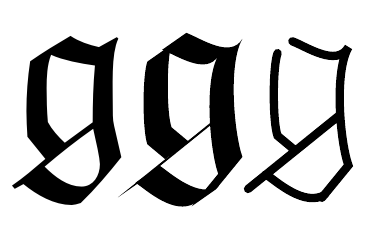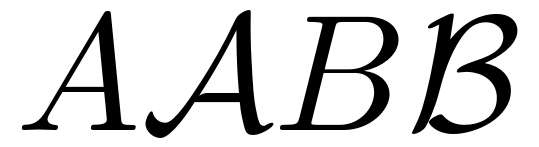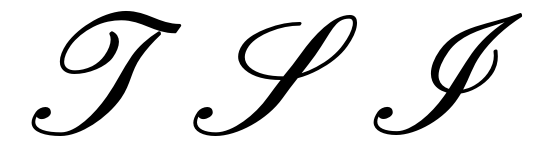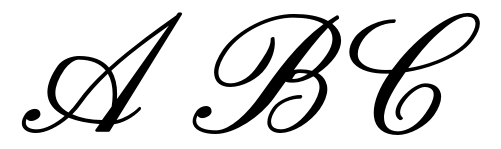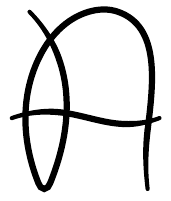Contents
At time of writing, the author was a professional mathematician and amateur calligrapher. His mathematical statements, of which there are none, should be viewed as reliable whereas his calligraphic comments, of which there are many, should not.
Abstract
It is a truth universally acknowledged, that a mathematician in possession of a good theorem must be in want of notation.
1 Introduction
It is almost as universally acknowledged that an alphabet of merely 26 letters is insufficient to express the vast richness of mathematical ideas. Whilst there may not be many articles that truly use more than 26 symbols, other factors weigh in to ensure that it is desirable to have a wide range to choose from. In particular, it is good style to use notation consistent with that of other authors in ones field, and to avoid notation that clashes. Notation should be used to aid comprehension, not to hinder it. Whilst there are times when it is appropriate for an author to say
I am sure that most readers would rather that he didn't.
A common practice in mathematical writing is to use similar letters for similar things. I find that my default assumption for the English alphabet is that of Table 1. ("Locally constant" means that when used then they should be considered as constant, but the constant is arbitrary.)
| Letters | Meaning |
| locally constant numbers, | |
| , | |
| functions, | |
| locally constant integers, | |
| too easily confused with , | |
| functions, | |
| variable real numbers, | |
| either vectors or the components of , | |
| either a vector or a complex number or function, | |
| variable real numbers, | |
| variable complex number | |
Table 1: The author's standard interpretation of letters
Your assumptions may be different; nonetheless, I would expect to see the same sort of grouping in that similar letters represent similar things.
This grouping is something that we have come to expect and is something that a good notation system can exploit. Using similar letters for things is a way of saying, "These are related.". But herein lies the problem for there are many types of relationship.
Let us consider two groups, and . Now for pairs of elements, and , we can ask whether or not there exists a homomorphism which takes to and to .
Here, we have several types of relationship. The two things designated and are similar things (they are both groups). The elements and are elements of , whereas and are elements of . The homomorphism is a third thing and so we have brought in a third alphabet and used the thing that most looks like a from that alphabet.
This illustrates a common strategy: when we have more than two types of relationship, we need to use more alphabets. The difficulty with this is twofold. Firstly, there may not be a clear correspondence between the new alphabet and the old; it is standard that represents and represents , but what represents ? Secondly, by using symbols from an unfamiliar alphabet we lose the quickness of association that familiar symbols bring.
An alternative is to use the same letters but from different typefaces. The choice of for an element of is actually an example of this. A more extreme example is the common notation for the Lie algebra of a Lie group: of .
In days of yore, this was self-limiting. Articles with fancy typefaces required careful handling, often with the symbols written by hand. In modern times, such archaic methods seem … archaic. With the plethora of typefaces available, it is possible to have a whole panoply of symbols all related and all in different typefaces.
This freedom does have a negative side. It is now possible to use obscure typefaces in articles and presentations. However, from time to time it is desirable to actually write a symbol by hand, either on a chalkboard or, dare I say it, a piece of paper. The temptation, when faced with a complicated symbol in a complicated typeface, is to replace them all by just "squiggle" (unicode character U+21DC). This is less than perfect as it breaks the relationship that the choice of notation was designed to preserve.
One can easily imagine an extreme case. A mathematician writes an article involving some concepts that he chooses to express using letters from a variety of typefaces; say , , , and . This mathematician is then asked to speak on that article and decides, either willingly or unwillingly, to present the material on a chalkboard. He then has to write these symbols on the board. One of the listeners to this talk likes to take notes. She then has to copy these symbols from the board to her pad of paper. Unfortunately, the speaker is a little indistinct, both in speech and writing, and the symbol is never clearly explained. So the listener writes down some approximation of it, but it is such a poor approximation that when she looks back at these notes six months later1 then it isn't clear if this symbol was , , or something else entirely.
1She's a very keen mathematician and actually reads again the notes that she makes.
In conclusion, to enjoy the freedom of the wide variety of typefaces available, mathematicians need to learn how to write these symbols both on the chalkboard and paper.
2 Calligraphy
The art of writing beautifully is called calligraphy. By using a little of this art of letter-forming, a mathematician can ensure that these strange symbols that she uses are clear both to others and, six months later on, to herself. There are many, many books that explain how to do calligraphy and which explain in detail how to form the letters. However, calligraphy for mathematicians is slightly different to calligraphy in general.
The major difference is in the materials used. Either this will be chalk on a board, or a normal pen on paper. Whilst an experienced calligrapher can produce beautiful works of art using driftwood for a pen, it is more usual to start with a special calligraphic pen. These come in two sorts: thick pens and thin pens. Thick pens are usually held at a constant angle and drawn across the page, never being pushed or turned. A thin pen (or a copperplate pen) is usually used in a more fluid manner and it is common to vary the pressure to change the thickness of the line. Examples of the type of stroke produced with each are in Figure 1.
The peculiarity of mathematical calligraphy is that whilst the typefaces are often designed to be written with a thick pen, the tools are closer in output to a thin pen as they produce a stroke whose width does not depend on the angle at which the implement is held. There is a further difference between chalk and a normal writing pen in that chalk is less amenable to being pushed: drawing a circle with chalk will usually require two strokes whilst with a pen only the one. A third aspect of chalkboard mathematical calligraphy is that it should, by design, be clear at a distance. Thus intricacies are to be severely frowned upon.
The problems are most acute for the chalk-wielder. She not only has to write an unusual symbol, it has to be clear from a distance (clear enough that the inexperienced note-taker can make a reasonable stab at copying it), and it has to look like a symbol from a typeface designed for a wholly different type of pen. No wonder many resort to squiggles!
3 The Fraktur Letter
The fraktur style, of which is an example, is one of the more common of the "fancy alphabets" in use in mathematics. It is therefore a reasonable choice for an example of showing how to go from a proper calligraphic letter to something suitable for a chalkboard. Let us begin with the letter itself, as displayed in Figure 2 next to a standard one for comparison.
What is clear from this is the angularity of the letter. Although individual lines may curve (the lowest stroke being the most obvious), major direction changes are sharp. When converting to a chalkboard style, these are the characteristics that we wish to preserve (even to exaggerate).
Let us begin by replicating the character in a calligraphic manner as in Figure 3. The left-hand rendering is the original character from the typeface, the middle is as if drawn with a calligraphic pen, and the right-hand version follows the same strokes but with an "ordinary" pen.
Now, while this is reasonably faithful, it is not suitable for a chalkboard. The thin line will be lost, and the angles could easily be smoothed out. The fact that the top left corner is continuous is a coincidence brought on by the thickness of the lines (this can be seen in the "skeleton" rendering). So we need to modify it to exaggerate the angularity, to make it feasible to draw on a chalkboard, and ensure that it remains distinct from the ordinary .
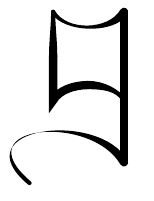
The top of the letter has a nice dip rising to a point at the right. We can emphasise that. This is matched by the thin line at the bottom of the main part of the letter, but the thinness will be lost when rendered by chalk so we replicate (and mirror) the dip at the top. The side lines may as well be vertical. The top of the letter is now sufficiently angular, but the descender has no distinguishing features. A simple remedy for this is to make it sweep up instead of down. This also means that there is plenty of space for an exaggerated swash if so desired. The result is in Figure 4.
Whilst this can no longer be called fraktur, it has the same angularity and thus will be clear on a chalkboard.
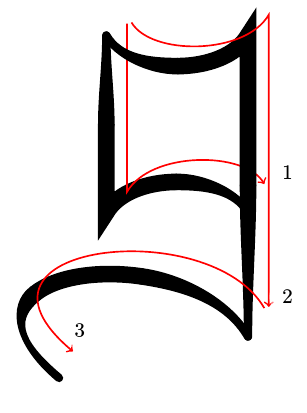
Seeing and writing are two different things. Fortunately, the construction of the letter allows us to see how it should be written as in Figure 5.
This is a letter which is clearly distinguishable from an ordinary "" and which is simple to write. It is therefore suitable for using on a chalkboard.
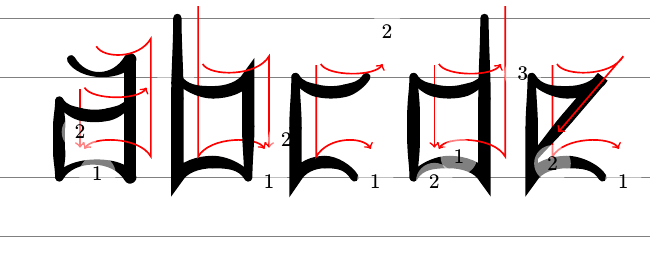
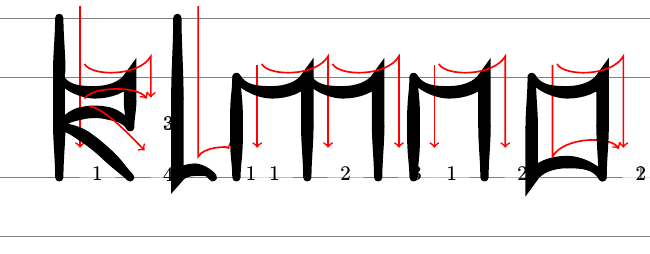
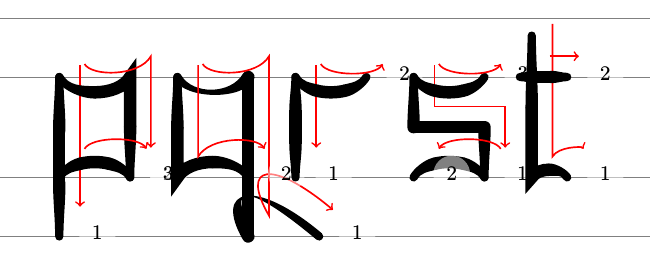
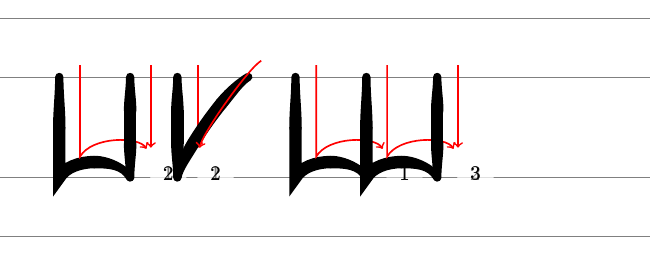
The characteristics of this letter are obvious. The verticals are decidedly vertical and the horizontals have a definite arc which goes in the obverse direction to the expected one. These combine to create the angular effect. We can apply these principles to the entire alphabet to produce a legible "mathematicians fraktur" wherein the letters are close enough to their "true" forms that their meaning is apparent, and are simple enough that this meaning is conveyed even when they are drawn in chalk on a chalkboard. Only the "x" proves disappointing, due to its lack of any horizontal or vertical lines.
A full lowercase rendition of "blackboard fraktur" can be found in Appendix A.
4 Script Capitals
The other typeface favoured by chalk artists is the script typeface, primarily in uppercase. The difficulty with this typeface is that there is both a danger of not making it sufficiently ornate and of making it too ornate. If we use LaTeX fonts, we can see in Figure 6 that the letters produced by \mathcal are not sufficiently distinguishable from ordinary letters to be usable on a chalkboard. At the other extreme we have \mathscr where, as shown in Figure 7, some letters are so ornate that it is hard to tell what they are.
As with the fraktur typeface, the goal is to find a characteristic of such letters that clearly identifies the typeface and can be replicated easily whilst not obscuring the letter. With fraktur letters, it is the angularity that is distinctive. Let us look at a few characters from the \mathscr font where we can tell what the letter should be, see Figure 8.
The exaggerated lean of the characters is certainly characteristic of this typeface, but is also hard to clearly reproduce. There are few chalk aficionados who attempt to use the distinction between and (or even ) on a chalkboard so using the lean to distinguish between and is probably insufficient. More visually robust is the loop that accompanies most characters (the "M" and "N" are the notable outliers here: and ). Thus our solution is to add a loop to all the letters. Again, the goal is to make a typeface that is instantly recognisable and easy to reproduce so we make the loop as uniform as possible across the alphabet. For most letters we can choose to make it either the initial upright or, for the curved letters, part of the top. For a few, such as the "H", then practicality weighs in and the loop is slightly altered from what one might expect. The letter "A" is seen in Figure 9 and a full uppercase alphabet2 in Appendix B.
2Created as a font using iFontMaker.
5 Mathematical Calligraphy
Thus far the term mathematical calligraphy has meant "calligraphy for mathematicians". That is, how can a little knowledge of calligraphy aid the generic mathematician. Another interpretation, and probably the one that initially comes to mind, would be of mathematically inspired calligraphy. There are, perhaps surprisingly, few examples of this. Whilst it is not hard to devise a typeface with some connection to mathematics3, to qualify as mathematical calligraphy then it should be a reasonable task to form the letters using a pen.
3There is, apparantly, a phase every typeface designer goes through wherein they design a typeface based on ruler-and-compass constructions. A modern (and beautiful) version of this can be found in the online book A Constructed Roman Alphabet. I've also experimented with mathematical lettering as can be seen in the documentation of the braids and TQFT packages. Perhaps one day the definition of a braid will be written as a braid itself. But I digress.
Given the dearth of such examples, we can begin at the begining with numbers. Here, then, we present a mathematical typeface suitable for calligraphy designed with numbers in mind. The full alphabet4 is presented in Appendix C. The inspiration behind it came from writing the word:
4Created using iFontMaker. Unfortunately, I have lost my original construction of this typeface and I'm not sure I remembered all of the assignments correctly. Any suggestions for improvements will be gratefully received.
Mathforge
This does give a whole new dimension to the idea of encoding formal arithmetic as numbers. As an example consider the following statement (taken from Wikipedia).
In set theory, which is capable of acting as an axiomatic foundation for modern mathematics, natural numbers can be represented by classes of equivalent sets.
The Holy Grail for this typeface would be to find a statement of the form:
This sentence is its own Godel encoding.
A Chalkboard Fraktur


B Script Capitals
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
C Numerical Typeface
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
a b c d e f g h i j k l m n o p q r s t u v w x y z
D Drawing the Fraktur Font
Here's an animation of how to draw the Fraktur Font.