1 Introduction

In my post on Colouring Origami I looked at various options for designing a modular origami Platonic solid. In this, I used the fact that, mostly, the modules in such an origami model correspond to edges in the polyhedron. Therefore selecting different colours or patterns1 for the modules corresponds to an edge colouring of the polyhedron.

However, life isn't always that simple. Some origami modules have an interesting feature which is that the colour that they are made of is all but invisible on the edge to which they correspond. Rather, they appear as part of the design on the neighbouring edges. The reason for this is, usually, due to how they interlock. The module has to overlap its neighbours in order to connect with them, and the ends of the module usually end up on top.

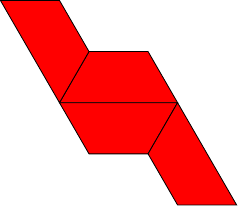
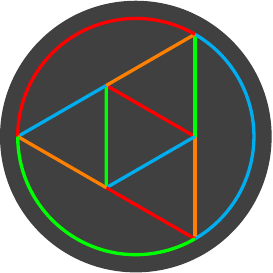
An example is shown in Figure 1. It is made up of four triangles, two in the middle with the light background and then two with the grey background and white circles. The edge that this module corresponds to runs across the centre of the design, but the two central modules will actually be hidden and this module will contribute the white circles to the final design. This can be seen in Figure 2 where three modules are connected together. The white circles in the centre are contributed by the two side modules, not the central one.

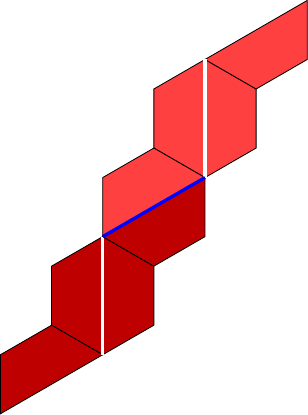
We can simplify the module a bit to look like the diagram in Figure 3. The triangles are trimmed slightly to emphasise which sides are the edges of the model. The module then corresponds to the edge down the middle, and it may seem that the colour of the paper is visible in the patches along that edge. But when the modules are fitted together then actually it is the ends of the module that end up on top, as in Figure 4.

This means that the colouring arrangements of the Colouring Origami post aren't as aesthetically pleasing because the designs are displaced relative to their respective edges.

The purpose of this post is to examine this situation and describe a colouring system that works in this case. To whet your appetite, here's an icosahedron made with this strategy.

2 Zig-Zags

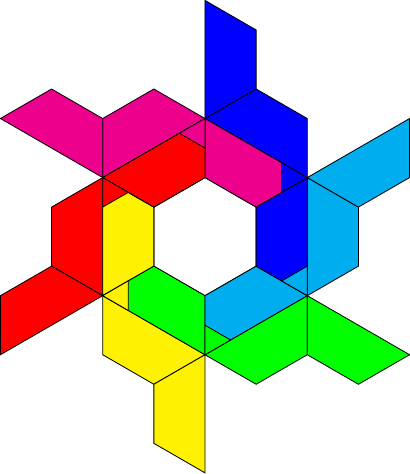
The key to this situation is to note that the edges where the design appears are the next edges round from the edge associated to the module, both in the same direction. With the module as above in Figure 3 then it is the next edge anti-clockwise incident to each end of the main edge. This produces a zig-zag style pattern, where edges of the same design are at the ends of a Z shape, as in Figure 6. In that figure the modules are meant to be the same colour, but are given slightly different tints to distinguish them. The thick white and blue lines represent the edges of the polyhedron.

The vertical white lines are the edges that each module represents. However, it is the central blue line that appears to have the red(ish) colour from the modules because that is where that colour is visible. Either side of the vertical white lines will be some other colour from other modules.

To make sure that the edge represented by the blue line is monochrome, both the modules that provide its colour have to be the same. This means that once a module is placed, various other modules must have the same colour and these must follow a particular design around the model whereby an end of one lies along the same edge as an end of the next.

Therefore, to see how to design a polyhedron with this type of module it is sufficient to trace out these zig-zags and place the modules accordingly. This is actually very restrictive and, as we'll see, produces essentially one design per polyhedron.

It is worth noting that each edge in the polyhedron is thereby associated with three separate modules. There is the module that represents the edge itself, and then there are the two modules that give it its colour.

3 Tetrahedron

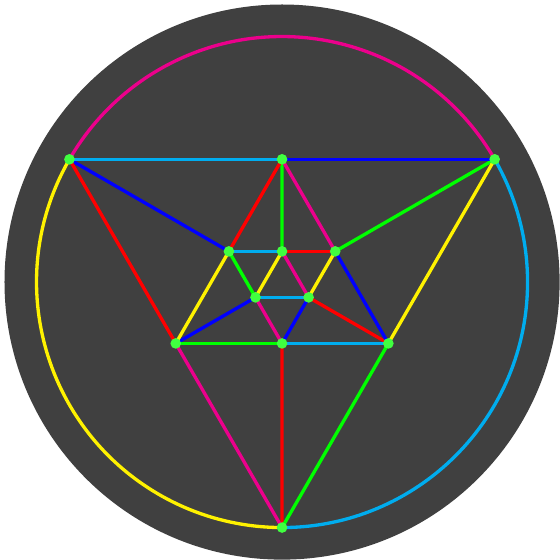
As in the original Colouring Origami post, I'll look at the tetrahedron in more detail than the other polyhedra. In Figure 7, the white lines represent the edges of the tetrahedron, with the viewpoint being looking at a vertex and the outer circle comprising the edges forming the opposite face.

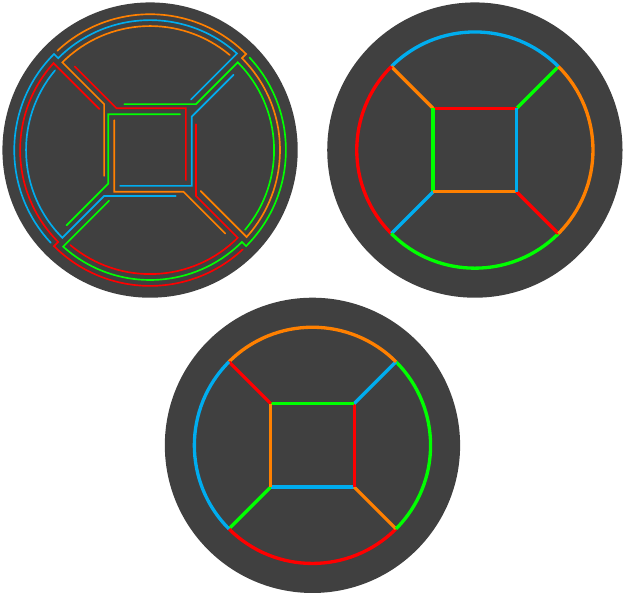
The coloured lines represent the modules, each of the six being a different colour. So each white line has three colours associated with it: the central colour that runs underneath it which is the edge that actually corresponds to it, and then the two colours either side which are the colours that are actually seen.

From Figure 7 we can see how the module colours must match: at each edge, the colours on either side must be the same. From this, we can see that the red and cyan modules must be the same, as must the blue and yellow, and the green and magenta. These are the only matches required, since the modules have the same matches at each end, so this uses (at most) three colours.

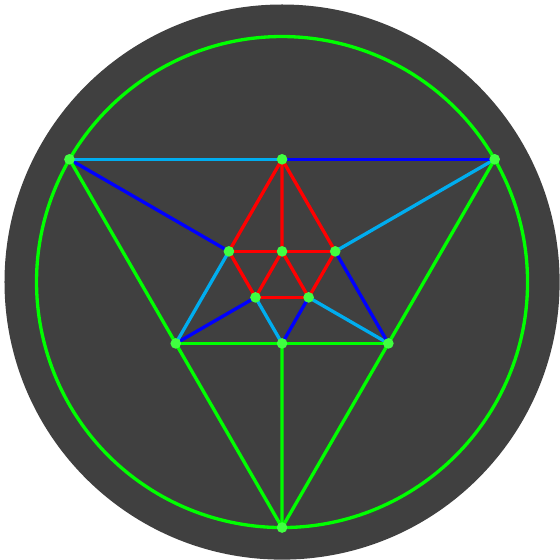
The edges that must be the same colour are opposite each other on the tetrahedron. Figure 8 shows this scheme. The upper left matches Figure 7 and the upper right shows the same but in a simpler diagram. The lower diagram shows the apparent colouring of the tetrahedron. This is the colouring that will actually be seen, and so is derived from the upper left diagram by taking the outer colours at each edge. Comparing this with the upper right shows that to get from the actual to the apparent colouring simply requires a rotation about the central vertex, or a cyclic permutation of the colours.

Cube

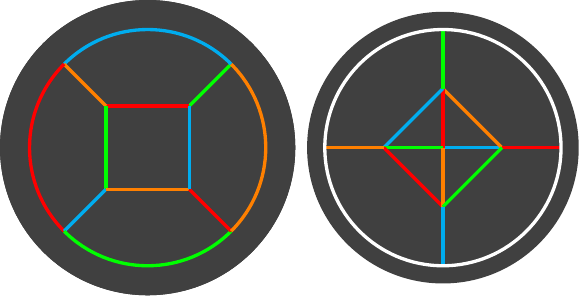
Figure 9 shows how to colour a cube. The diagram at the upper left has the detail of the modules, while the one at the upper right shows just the edge colours. The lower diagram shows the apparent colouring of the cube. Interestingly, each edge has the property that its actual colour is the same as the colour visible on its opposite edge.

Note also that this uses a maximum of four colours.

Octahedron

Figure 10 contains the colouring scheme for an octahedron.

As with the cube, this uses a maximum of four colours. It also has the same property that the apparent colour of an edge is the same as the real colour of its opposite.

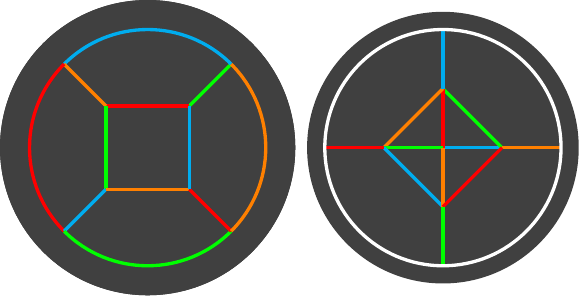
An octahedron is, of course, dual to a cube. Figure 10 shows the scheme in the most suitable way for the octahedron itself, namely centred on a face, but to compare it with the cube we need to recentre it on a vertex, as in Figure 11. In this diagram the white circle around the octahedron should be thought of as a single vertex, so that the edges that touch it are actually incident to the same vertex.

When comparing the octahedron and the cube then each edge in, say, the diagram of the cube corresponds to an edge in the diagram of the octahedron that is in roughly the same location and roughly perpendicular.

In Figure 11, the colours on the octahedron have been chosen so that at the central vertex they match the colours on the central face of the cube. At first sight, this matching does not appear to extend to the other edges of the cube and octahedron. However, if we imagine folding the modules in the opposite way so that the zig-zags go clockwise instead of anticlockwise for the octahedron then we get Figure 12 and we can see that the colours do match.

Incidentally, the tetrahedron is self-dual and its colouring is also self-dual in the sense that swapping the modules for their mirrors is still a valid colouring of the tetrahedron.

We shall explore the relationship between a polyhedron and its dual a little later in this article.

4 Dodecahedron

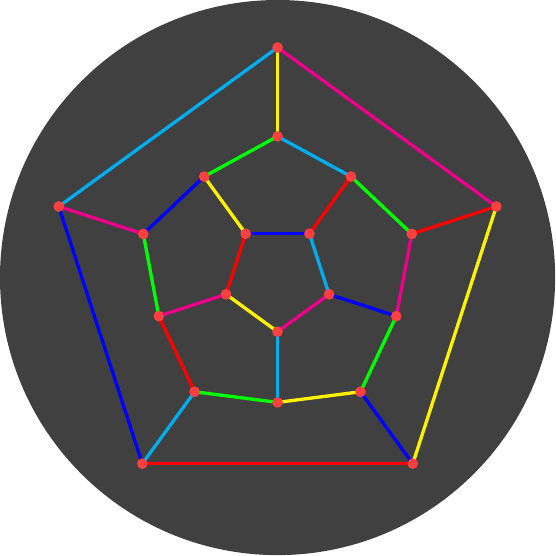
The colouring scheme for the dodecahedron is shown in Figure 13.

There is a phenomenal amount of symmetry in this design, some quite subtle and some relatively overt. Rather than try to go through all of it (and, no doubt, miss some), I'll just highlight one that I think is brought out well by this design.

In Figure 13, the green edges go around an "equator" of the dodecahedron. They alternate with each of the other colours: reading from the top and going anticlockwise then the sequence is green, blue, green, red, green, yellow, green, magenta, green, cyan. In the actual model, though, these alternate edges are the ones that have the apparent colour green. So the full equator is traced by the edges that are actually green and those that are apparently green.

Now some origami modules have the property that while the main colour for an edge is set as described in this article then the actual edge colour is visible in some part, it just isn't the dominant colour. I've hinted at that in Figure 4 where a small corner of each edge gets coloured by the edge colour. When a module like this is used to build the dodecahedron then an equator can be easily traced by looking for all hints of, say, green on an edge.

A symmetry argument shows that the same is true for the other colours, just that Figure 13 is set up so that the equatorial nature of green is the most evident.

5 Icosahedron

The colouring scheme for the icosahedron is described in Figure 14. All that has been said about the dodecahedron can be said also about this design.

The equators are less obvious in this layout but they are still there. For example, there is a (slightly deformed) pentagon formed by the five triangles that meet at the top of the central triangle. The blue edges form an equator around this pentagon. Figure 15 illustrates this. The red edges form the pentagon, and the green form the antipodal pentagon. The blue edges are from the colouring, and the cyan are the edges that appear blue on the model.

6 Some Design Considerations

When creating models based on these designs then there were a few things that I noticed that I think are worth recording. My favourite model is the icosahedron.

• The icosahedron uses six different colours or patterns. This can make it hard to see what is going on. The first model I made using this scheme used monochrome patterned paper. I felt that this worked well overall, but the design was not too evident.

  Then I made a model using coloured patterned paper and I felt that it was just too busy. Not only was the design not clear, even the way that the patterns were combined didn't look good. But there's no obvious grouping of the colours, meaning that it isn't possible to, for example, pair up the colours to reduce the busy-ness.

  The design I ended up with, then, to illustrate this design was to use two sets of patterned paper with one pattern being used for one colour and the other pattern for all the rest. This also highlights the equatorial nature of the pieces of the design. The module I was using (Sky Star Kusudama from the Zen Origami book) also had the feature that the underlying edge colour is shown so this makes the equator really visible.

• When using patterned paper then it can be that the pattern is not symmetric on the paper. Unless the modules are all folded the same way then this can lead to the edges not all being the same. This is the sort of thing that will probably only be noticeable to the person creating the model, and also probably only be irritating to that person. If, then, you are the sort of person that would notice it and would be annoyed by it then it is worth thinking about it ahead of time. I found that I couldn't work out the way to start folding a module just by looking at a completed one, so – for the Sky Star Kusudama module – I folded the first fold for all the pieces of paper first (this first fold then determined the orientation of the module).

• Following on from that last point, with non-symmetrical paper then the modules can have an orientation. That is, the patterns on the two parts that are shown are not identical. So when putting one module in the model you can either put it so that it is opposite to an existing module or the same.

  One way to visualise this is to think of a module as an arrow. Putting them head-to-tail means that when putting in a module, the visible part is the opposite to what is already there. Whereas head-to-head and tail-to-tail means that the visible part is the same as what is already there.

  For all but the tetrahedron then there are an odd number of modules for each colour meaning that it isn't possible to use the head-to-head and tail-to-tail throughout. So if consistency is sought, the only option is head-to-tail.

7 Ribbon Graphs

And now for a bit of maths.

In showing these designs, both in this article and its companion Colouring Origami, I've made a lot of use of graphs to show the structure. These graphs are planar graphs meaning that they can be drawn without edges crossing, and to show them then I've used a plane embedding of each graph. Such embeddings arise naturally from considering their origin as the edges and vertices of polyhedra.

In Colouring Origami then all that was needed was the graph structure: the embedding into the plane was for illustration only. In this article, on the other hand, then the plane embedding has been needed because we've used more structure than just where the edges meet. The extra structure that we've needed is that at each vertex then we've known how to go from an edge to the next one around. This can be inferred from a plane embedding, but then it depends on that embedding and isn't a inherent to the graph itself. So what we want is an abstraction of that data which can be used to augment the graph structure. This is a known structure.

That definition needs a little work to be made precise in all circumstances. There is an issue when the graph contains loops (edges with both ends incident at the same vertex) since then the cyclic ordering needs to take into account both ends of the edge. It is therefore better to work with half-edges than full edges. In fact, the entire structure of the ribbon graph can be encoded by considering half-edges.

Let us consider how to build a ribbon graph starting with a set of half-edges. Firstly, each half-edge needs an associated other half. This defines a pairing on half-edges, and obeys just a couple of rules. No half-edge can be its own other half, and if we start with a half-edge, take its other half, and then take the other of that other half then we should get back to the original half-edge.

Mathematically, we encode that by a function on half-edges that is a fixed point free involution.

Secondly, at each vertex we want a cyclic ordering. We can consider this as a way of finding the next half-edge around that vertex. Since each half-edge has a single vertex at its end, there is no ambiguity in using this to define a "next half-edge" – when dealing with a full edge then we need to specify which vertex we're rotating around but half-edges have only a single vertex. So the cyclic ordering at each vertex defines a global "next half-edge" assignment on the set of all half-edges. There's only one requirement on this assignment, which is that it is reversible so that we can also always find the previous half-edge.

Mathematically, we encode that by a function on half-edges that is invertible.

This function then determines the vertices so we don't need to add them as extra structure. The way that this works is as follows: start with a half-edge and consider the set generated by taking that half-edge, its next half-edge, the next of that one, and so on (this is called an orbit). Doing this with all half-edges partitions the set of half-edges into distinct parts, each of which corresponds to a vertex. So the vertices are these orbits.

Our graphs will be finite, in which case the orbits just need to be closed under $\sigma$. The requirement of being closed under ${\sigma }^{-1}$ is only needed if the orbits could be infinite.

Now let us consider how to formalise colourings. Colours are just words, so a colouring of a graph is an assignment of a label to each edge, which is a function from the set of edges to a set of labels. Now, each edge is made up of two half-edges so we can also consider a colouring to be an assignment of a label to each half-edge with the property that if two half-edges belong to the same edge then they have the same colour. This will be the most useful way to view a colouring.

Now choosing colours for the zig-zag modules defines a colouring for the ribbon graph. But the point of these modules is that the colour of the edges is actually seen elsewhere on the graph. Each module contributes half the colour for its neighbouring edges, so we can think of this as the colour for its neighbouring half-edges. So if we consider the representation of the modules as in the tetrahedron in Figure 7, as on the left in Figure 16, then we adjust it slightly to shorten the ends so that they look like half-edges, as on the right.

So the zig-zag modules cast the colours from the edges to the neighbouring half-edges. Given a colouring, $c:G\to C$, then the apparent colour of a half-edge, $e\in G$, is the actual colour of the previous half-edge. This means that the apparent colouring is $c\circ {\sigma }^{-1}$. What we want is to choose the original colouring so that this apparent colouring is a genuine colouring.

Zig-zag colourings exist, since a monochrome colouring is a zig-zag colouring.

The main result for zig-zag colourings is the following.

These initial zig-zag colourings are what we have been identifying for the various polyhedra.

The other interesting aspect of this colouring is how it interacts with duality. A ribbon graph has a natural notion of a dual, which is closely related to the duality of polyhedra. Since we have defined our ribbon graphs using half-edges, together with the pairing of half-edges into edges and the permutation that defines the next half-edge, then to define the dual we need to transform this structure.

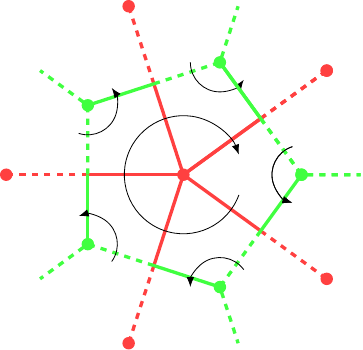
To see how this works, consider the dual of part of a graph with a plane embedding. In an embedding, we place a new vertex in each region and join the vertices if their regions share an edge. This means that the edges in the original graph and its dual correspond, so the underlying set of the half-edges in the dual is the same as in the original. Moreover, the assignment of the other half is the same in both. So the only thing that changes is the "next half-edge" assignment.

Consider Figure 17. The solid half-edges correspond, so to figure out the structure we look at the order of these half-edges around the new vertex. As we trace the green half-edges around the new vertex, we go from one to the next by applying $\iota$ to get the other half and then applying $\sigma$. So the new "next half-edge" function is $\sigma \circ \iota$.

What is also evident from Figure 17 is that in the plane embedding of the graph then if we put an anti-clockwise ordering around the original vertices, then on the dual we need to put a clockwise ordering around the vertices of the dual. This is the same behaviour as seen at the "Magic Roundabout" in Swindon where traffic going the correct way around the outer roundabouts results in it going the "wrong" way around the central one. This is why the colourings of, for example, the cube and octahedron need to use opposite modules to be truly dual.

The main result for us is that a zig-zag colouring of a ribbon graph gives a zig-zag colouring of its dual.

The extra structure on a ribbon graph means that it can also mimic other aspects of polyhedra, such as truncation and stellation, and so are a good context to investigate how these interact with zig-zag colourings. That's for a future investigation.

For now, I'm just intrigued that a mathematical concept I first learnt about in a totally different context has cropped up in one of my recreational investigations.