Counting Fermat

loopspace

2018-09-18

Home
1. Introduction
2. Like Father, Like Son
3. Categorically Speaking
4. Hunting the Snark
5. Exploiting the Identity
1. 5.1. From $N$ to $R$ and $B$
2. 5.2. From $R$ and $B$ to $N$
6. Three or more
7. Whither Generalisation?
8. Conclusion

1 Introduction

The Math with Bad Drawings author, Ben Orlin, recently posted something about Fermat's Last Theorem that caught my eye. He used it as an example of how Mathematicians often find it useful to translate a concept from its original home to a different context to get some fresh insight on it.

He does this by recounting a way to recast Fermat's Last Theorem into Combinatorics, the area of Mathematics that deals with counting things. He shows that Fermat's Last Theorem is equivalent to counting two things being always different (I'll go into more detail in a moment). In the comments, Ben's father chimes in with a simpler way to express the counting.

This is very much a follow-up to that post. In it, I want to focus on a few aspects. I completely agree with the underlying point of Ben's article: that recasting an idea in a different context is an extremely useful tool in a Mathematician's toolbox, and I want to expand on it somewhat. To do that, I want to delve a little deeper into the recasting of Fermat's Last Theorem.

The spark for this post comes from a minor niggle with Ben's article. When I read it, my reaction was "That's cute … but … hmmm.". The difficulty I have with it is that Fermat's Last Theorem translates to "two things aren't equal", but without some reason to believe that they might have been equal in the first place, the revelation that they aren't equal lacks a bit of punch.

So I'd like to start by putting in a gentle punch.

2 Like Father, Like Son

Let's look in a bit more detail at the reformulations of Fermat's Last Theorem. If you've read Ben's article, and his father's addendum, you can skip a bit here.

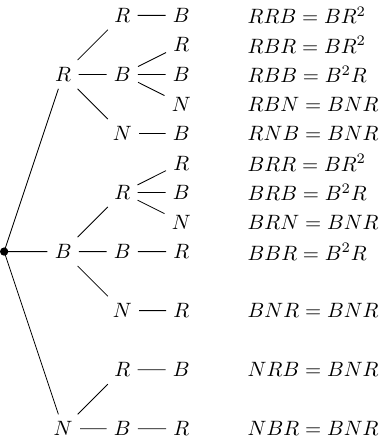
Imagine you have a number of distinguishable boxes, say $n$ of them, and a number of bins to put them in. The bins are either red, blue, or have no colour. Let's say that there are $T$ in total, of which $R$ are red and $B$ are blue. You can put as many boxes into a bin as you like. We call an arrangement of boxes in bins non-coloured if every box is in a non-coloured bin. We call an arrangement two-coloured if at least one red bin and one blue bin have at least one box in them.

The reformulation of Fermat's Last Theorem is: if $n > 2$ then the number of non-coloured arrangements is not equal to the number of two-coloured arrangements.

The demonstration of this is to show that the number of non-coloured arrangements is $(T - R - B)^{n}$ , while the number of two-coloured arrangements is $T^{n} - (T - R)^{n} - (T - B)^{n} + (T - R - B)^{n}$ . A bit of rearrangement says that these two are equal if and only if

T^{n} = (T - R)^{n} + (T - B)^{n}

Ben's father's reformulation is to define monochrome arrangements as those which are either all red or all blue. Then Fermat's Last Theorem says that the number of non-coloured arrangements is never equal to the number of monochrome arrangements.

An alternative reformulation, which we will return to later, is to note that $T^{n}$ is the number of all combinations, while $(T - R)^{n}$ is the number of non-red combinations (i.e., those that don't involve red bins) and $(T - B)^{n}$ of non-blue combinations. Then Fermat's Last Theorem says that for $n > 2$ , the total number of combinations is never equal to the number of non-red combinations plus the number of non-blue combinations.

3 Categorically Speaking

I should say at the outset of this section that Ben makes it quite clear in the article that this is just an example of such a reformulation and that he doesn't have any expectation that this will lead to a new proof of Fermat's Last Theorem, or even any particular insight into it. So the fact that I'm left with a feeling that there's something missing is purely in my own mind and not a reflection on the original article at all.

Nevertheless, I am left feeling as though the story is not complete. When I'm told that two things aren't equal, my reaction depends on whether or not I expected them to be equal. Given that most things in the world aren't equal to each other, my I tend to default to "not equal" so being told some things aren't equal does not shock me.

This is made even starker by Jim Orlin's formulation. There seems to me to be no reason at all to expect that the number of monochrome arrangements and non-coloured arrangements should be equal, since there is no relation whatsoever between the number of non-coloured bins and the numbers of red and blue bins.

In fact, I consider Jim Orlin's version to be so close to the original that I'm not going to consider it. To take this back to the underlying purpose of this and Ben's articles, when translating something from one mathematical context to another, the hope is that the new context reveals something fresh. To my non-combinatorial eye, Jim Orlin's version is so close to the original that my gut feeling is that any insight it reveals from the combinatorial side will have a direct analogy in number theory and therefore (in such a well-studied problem) be already known.

I therefore want to focus on the original version that Ben expounds. Now, when I see that two things are equal then I expect there to be some reason for that. In the context of counting, I either expect there to be two different ways of counting the same thing (for example, showing that $2 \times 3 = 3 \times 2$ ) or a function from one set to the other putting the two in a one-to-one correspondance.

Putting all that together, to say that two things are not equal and for that to mean something, there should be something that would give me cause to consider that they might be equal. At the least, I would like there to be a function from one set to the other which could plausibly be an isomorphism.

Note that Fermat's Last Theorem is saying that no such function exists, so in asking for a potential function I'm weakening the statement slightly. Rather than saying "they are not equal", I'm asking for "this reasonable attempt at making them equal fails" which is a bit weaker.

4 Hunting the Snark

The difficulty with trying to find something that doesn't exist, is that it doesn't exist. So to figure out what the mystery function might be, we need to look at the situation where it does work, namely when $n = 2$ . In this case, the number of non-coloured arrangements is the same as the number of two-coloured ones.

Let's see why that is so, and in so doing why Ben's version gives us a different view. We have the total, $T$ , number of red, $R$ , and number of blue, $B$ . Let's introduce $N$ for the number of non-coloured bins, then:

T = N + R + B

For the non-coloured arrangements, we have two objects (which can be distinguished) and $N$ bins to put them in. So we have $N$ choices for the bin for the first object, and $N$ choices for the second, making $N^{2}$ in total.

Now a two-coloured arrangement must have one object in a blue bin and one in a red bin. As we only have two boxes, this leaves us with two possibilities: first in a blue bin and second in a red bin or first in a red bin and second in a blue bin. This yields $B R + R B = 2 R B$ arrangements.

So for an arrangement with equal numbers of two-coloured and monochrome arrangements, we must have:

N^{2} = 2 R B

Finding $R$ , $B$ , and $N$ satisfying that is easy (we will look at this more closely in the next section).

Once we have such $R$ , $B$ , and $N$ then the equation for Fermat's Last Theorem (aka a Pythagorean Triple) is:

\begin{aligned} T^{2} & = (T - R)^{2} + (T - B)^{2} \\ or & = (N + B)^{2} + (N + R)^{2} \end{aligned}

Note that if $R$ and $B$ share a common factor, then the resulting triple is not primitive so we could concentrate on those where this isn't the case. Also, expanding out the brackets in the lower identity shows – after much cancellation – the relationship to the identity $N^{2} = 2 R B$ .

It's also easy to see that any Pythagorean triple, say $(a, b, c)$ with $c^{2} = a^{2} + b^{2}$ , arises in this fashion by putting:

\begin{aligned} R & = c - a \\ B & = c - b \\ N & = a + b - c \end{aligned}

This therefore gives rise to a method for generating Pythagorean triples. I certainly wasn't aware of this particular method before, so if nothing else then I've learnt something new about Pythagorean triples.

5 Exploiting the Identity

We have the identity $N^{2} = 2 R B$ which is equivalent to the existence of a Pythagorean triple. Let's see how this gives an isomorphism between non-coloured and two-coloured arrangements.

There are two routes to take. One starts with choosing $N$ and then picks $R$ and $B$ to suit, the other starts with $R$ and $B$ and picks $N$ to suit. Clearly there will be some restrictions, so let's establish them first before exploring both routes.

Let's start by fixing $N$ . Then we need to choose $R$ and $B$ such that $2 R B = N^{2}$ . Clearly, therefore, $N$ needs to be even. With that restriction, we just need to look at factor pairs of $N^{2} / 2$ to find candidates for $R$ and $B$ .

In the other direction, we need to choose $R$ and $B$ so that $2 R B$ is a perfect square. To make this a bit shorter, we'll look at the special case where $R$ and $B$ are coprime (i.e., have no non-trivial common factors). In this case, since $N^{2}$ is even, $N$ is even, and so $N^{2}$ is divisible by $4$ , whence one of $R$ and $B$ must be even. With our assumption, this means exactly one is even and wlog let us assume that $B$ is even. Then playing around with prime factorisations, it can be deduced that $R$ is a perfect square and $B / 2$ is a perfect square. This means that there are numbers $r$ and $b$ with the property that $R = r^{2}$ , $B = b^{2} / 2$ , and $N = r b$ .

The assumption on $R$ and $B$ being coprime will mean that $r$ and $b$ are also coprime, but in fact any pair $(r, b)$ will lead to a valid solution of $N^{2} = 2 R B$ . It is, however, not the case is that we get every possible solution from such pairs but it is the case that we get all solutions which give primitive Pythagorean triples.

5.1 From $N$ to $R$ and $B$

Let us look at how to combinatorially see how to relate $N^{2}$ to $2 R B$ with $N$ as the starting point.

The $N^{2}$ is clearly the number of non-coloured arrangements. We can think of it as a square of sides length $N$ , as in Figure 1. The dot at position, say, $(3, 4)$ represents the first box in bin $3$ and the second box in bin $4$ .

Figure 1: A grid of $36$ dots

The next step is straightforward: we cut this in half. The obvious way to do this is to cut it parallel to one side, as in Figure 2, which we know we can do because $N$ is even. In the example, the first box is only allowed in one of the first $3$ bins.

Figure 2: A grid of $18$ dots

We now choose a factorisation of $N^{2} / 2$ . There's an obvious one, which is $R = N$ and $B = N / 2$ , but any factorisation will do. This gives another way to draw the same dots in a rectangle. Figure 3 shows it for the factorisation $18 = 2 \times 9$ .

Figure 3: A rearranged grid of $18$ dots

When we do the rearrangement, we want to do it in such a way that we know which new dot corresponds to which old dot (as indicated by the colours in Figure 3). In this new rectangle, we assign the sides as $R$ and $B$ . Then a point in this new rectangle corresponds to a box in a particular red bin and another box in a particular blue bin. The two halves of $N^{2}$ then correspond to whether the first box is red or blue.

We therefore have our correspondance: a two-colour arrangement defines a point in the rectangle $R \times B$ , which maps across to a point in the half rectangle $N^{2} / 2$ . If the first box is in a blue bin, we shift it to the second half rectangle.

5.2 From $R$ and $B$ to $N$

Now let us consider the opposite direction, namely where we start with $R$ and $B$ and these determine $N$ . Recall that we're working with a special case which means that we actually start with two numbers $r$ and $b$ with $b$ even and set $R = r^{2}$ , $B = b^{2} / 2$ , and $N = r b$ .

The combinatorics is straightforward here. We will illustrate as we go along with $r = 3$ and $b = 2$ . We start by forming a $b \times b$ –grid of squares each containing an $r \times r$ –grid of dots, as in Figure 4.

Figure 4: A Grid of a Grid of Dots

Since $N = r b$ , there are $N^{2}$ dots in this grid. Thus picking a dot corresponds to choosing two uncoloured bins, in order, and putting the first box in the first and the second box in the second.

There are $R$ dots in each inner grid, so choosing a dot in the picture also chooses a dot in an inner grid and thus picks one of the red bins. There are $b^{2} = 2 B$ inner grids, so choosing a dot in the picture also chooses an inner grid which corresponds to a choice of one of the blue bins. That there are twice as many inner grids is accounted for in the same way as before: on the left-hand side then the first box goes in a red bin while on the right-hand side the first box goes in a blue bin.

6 Three or more

Let's look at this with three boxes, so $n = 3$ . The number of monochrome arrangements is straightforward to work out: it is just $N^{3}$ . The number of two-colour arrangements is slightly more complicated, as there are now several different combinations with two-colours. These are illustrated in Figure 5.

Figure 5: Tree diagram of possibilities with $3$ boxes

Adding up all the possibilities, we arrive at the sum:

3 B^{2} R + 3 B R^{2} + 6 B N R = 3 B R (B + R + 2 N)

Thus Fermat's Last Theorem with $n = 3$ is equivalent to saying that there are no integer solutions to:

N^{3} = 3 B R (B + R + 2 N)

Even before we look closely at this, we can see it is a notch more complicated than the case for $n = 2$ . We have $N$ on both sides, so we can't fix $N$ and work out $B$ and $R$ as we did before.

I'm not used to studying such equations, so I don't have a range of tactics to try. I'm neither a combinatorialist nor a number theorist so beyond writing a computer program to try things out, I have no particular insight to offer here. My first thought would be to look for prime factors, but that feels as though it drags us back to number theory (indeed, my few attempts along those lines did seem to lead me back to finding solutions of $x^{3} + y^{3} = z^{3}$ due to the presence of $B + R$ on the left-hand side).

Part of my hesitation to continue along this line is that this is such a well-known problem, and therefore so well-studied, which combines with my ignorance in both combinatorics and number theory to mean that I am extremely unlikely to stumble upon something fresh, or even to know that I have if I do so. What would be nice would be if there were a straightforward combinatorial argument that said that Equation 1 had no integer solutions – after all, special cases of Fermat's Last Theorem were solved by other means before the general proof came along. But, being not my area, I shall not spend time looking for it.

7 Whither Generalisation?

But I'm not done yet. One of the issues I highlighted above with Fermat's Last Theorem is that you are trying to prove that something can't happen, which is always difficult. That led me to consider the case where it did work, namely $n = 2$ . If we didn't know about Fermat's Last Theorem, we might be more inclined to look for similar cases that do work than those that don't. Thus rather than focus on Fermat's Last Theorem, let's look closer at the statement for $n = 2$ and see if we can generalise it a different way.

Our current statement is as follows. Let $R$ be the number of red boxes, $B$ of blue boxes, and $N$ of boxes with no colour. If the number of non-coloured combinations is equal to the number of two-coloured solutions, then

(N + R + B)^{2} = (N + R)^{2} + (N + B)^{2} .

Let's translate this statement back in to words. On the left is the total number of combinations. On the right, the term $(N + R)^{2}$ is the number of non-blue combinations while $(N + B)^{2}$ is the number of non-red combinations.

This suggests something. The usual way to count the total number of combinations would be to split them up according to number of colours: start with no colours, then those with one colour, and finally those with two colours. We can further split the ones with one colour into the monochrome and the ones with a mixture of that colour and non-coloured. This corresponds to the expansion:

(N + R + B)^{2} = N^{2} + (R^{2} + B^{2}) + (2 N R + 2 N B) + (2 R B)

But Equation 2 suggests doing this the other way around. Instead of counting the colours present, count the ones absent. The splitting is thus into those with no red, those with no blue, and those with no red or blue. This doesn't capture them all, for that we need to add those with all colours, and there is overlap since the set of those with no red or blue is the intersection of those with no red and those with no blue. The formula is bit more complicated, but in words it is: the total number of combinations is the number with both red and blue plus the number with no red plus the number with no blue minus the number with no red or blue. In symbols:

(N + R + B)^{2} = 2 R B + (N + B)^{2} + (N + R)^{2} - N^{2}

From this we easily see how $N^{2} = 2 R B$ leads to a Pythagorean triple.

7.1 Collapsing

Let's generalise, but further than the original. Let's have $n$ distinguishable boxes to put in bins which are either not coloured or coloured with one of $c$ colours. We'll label the colours $1$ to $c$ and use $0$ for the "non-colour". Let $b_{i}$ be the number of bins of colour $i$ . We will insist that each colour must be present, so we assume that each $b_{i} > 0$ . Then the total number of combinations is:

(\sum_{i = 0}^{c} b_{i})^{n}

We want to describe this using a similar tactic of splitting according to what colours are not present. To allow us to focus on the overall expression, given a set of colours $C$ (which can include $0$ for the non-colour), let us write $T_{C}$ for the number of combinations which don't use colours from $C$ . We will abuse this notation slightly by allowing us to drop the braces when writing a set explicitly, for example, using $T_{i, j}$ in place of $T_{{i, j}}$ and $T$ for $T_{\emptyset}$ . We also need a notation for those combinations that actually use all colours, let us write $\hat{T}$ for this. Note that this isn't $T_{\emptyset}$ .

There are straightforward formulae for the $T_{C}$ :

T_{C} = (\sum_{i \notin C} b_{i})^{n}

The formula for $\hat{T}$ can be quite complicated, but there are two special cases that are simple. If there are more colours than boxes, $\hat{T} = 0$ . If there are the same number of colours as boxes, so $n = c$ , $\hat{T} = c! b_{1} \dots b_{c}$ .

The inclusion-exclusion principle says that:

T = \hat{T} + \sum_{i = 1}^{c} T_{i} - \sum_{i < j} T_{i, j} + \sum_{i < j < k} T_{i, j, k} - \dots \pm T_{1, \dots, c}

(Note that $T_{1, \dots, c} = b_{0}^{n}$ .)

The existence of Pythagorean triples says that there are situations with $n = 2$ and $c = 2$ where lots of things in this cancel. Fermat's Last Theorem says that with $n > 2$ and $c = 2$ then there aren't any situations where analogous things cancel. This suggests studying the following situation.

Definition 1

For $n$ boxes to be placed in bins with $c$ possible colours, a choice of numbers of bins $(b_{0}, \dots, b_{c})$ is said to collapse at level $r + 1$ if, with the above notation,

T = \sum_{i = 1}^{c} T_{i} - \sum_{1 \leq i < j \leq c} T_{i, j} + \dots \pm \sum_{1 \leq i_{1} < \dots < i_{r} \leq c} T_{i_{1}, \dots, i_{r}}

Which leads to the following restatement of Fermat's Last Theorem.

Theorem 1 Wiles

For $n > 3$ and $c = 2$ , there are no choices of numbers of bins which collapse at level $2$ .

7.2 Sums of Cubes

If a solution collapses at level $2$ , then relabelling the terms in Equation 3 leads to an equation of the form:

z^{n} = x_{1}^{n} + x_{2}^{n} + \dots + x_{c}^{n}

which I strongly suspect has been well investigated as it is an obvious generalisation of the equation in Fermat's Last Theorem.

Let us, nevertheless, look at where $n = c = 3$ collapses at level $2$ . The collapsing condition is:

3! b_{1} b_{2} b_{3} + b_{0}^{3} = (b_{0} + b_{1})^{3} + (b_{0} + b_{2})^{3} + (b_{0} + b_{3})^{3}

Using a simple python script, I found several solutions that fit this, the first being:

(b_{0}, b_{1}, b_{2}, b_{3}) = (2, 7, 9, 10)

which can be verified as

\begin{aligned} 6 \times 7 \times 9 \times 10 + 2^{3} & = 3788 \\ (2 + 7)^{3} + (2 + 9)^{3} + (2 + 10)^{3} & = 3788 \end{aligned}

Substituting this into Equation 3 yields:

28^{3} = 18^{3} + 19^{3} + 21^{3}

As with Pythagorean triples, we can multiply everything by a constant to get a new solution so let us say that a solution is primitive if the $b_{i}$ (including $b_{0}$ ) are coprime. Continuing the search, we get the following as the first few primitive solutions:

\begin{matrix} (2, 7, 9, 10) \\ (2, 9, 16, 19) \\ (1, 9, 19, 24) \\ (5, 21, 24, 35) \\ (6, 21, 31, 32) \end{matrix}

(Interestingly, there seem to be quite a few solutions where the last two numbers differ by $1$ .)

7.3 Collapsing at the Last

A system collapsing at level $2$ is one extreme, the other would be it collapsing just before the end. With $n = c$ , we can consider collapsing at level $c$ or $c - 1$ . The sign alternation means that collapsing at level $c$ makes sense for $n$ even, and at $c - 1$ for $n$ odd.

For $n$ even (with $n = c$ ), the condition for collapsing at level $c$ is that:

n! b_{1} \dots b_{n} - b_{0}^{n} = 0

and this is quite easy to find solutions for. Note that putting $n = 2$ brings us back to the situation of Pythagorean triples.

For $n = 4$ , we have:

24 b_{1} b_{2} b_{3} b_{4} = b_{0}^{4}

To get solutions, we need the product $b_{1} b_{2} b_{3} b_{4}$ to complete $24$ to a $4$ th power. Since $24 = 2^{3} \times 3$ , the first way to do that is to distribute $2 \times 3^{3}$ amongst $b_{1}$ , $b_{2}$ , $b_{3}$ , and $b_{4}$ . For example, $2$ , $3$ , $3$ , $3$ . This works with $b_{0} = 6$ . Substituting back into Equation 3 yields the identity:

\begin{aligned} 17^{4} & = (15^{4} + 14^{4} + 14^{4} + 14^{4}) \end{aligned}

Another distribution is $1$ , $2$ , $3$ , $9$ , again with $b_{0} = 6$ . This yields:

\begin{aligned} 21^{4} & = (12^{4} + 18^{4} + 19^{4} + 20^{4}) \end{aligned}

For $n = 6$ a similar analysis says that we get some solutions by letting $b_{1}, \dots, b_{6}$ be built from $2^{3} \times 3^{4} \times 5^{5}$ . For example, $1$ , $9$ , $10$ , $15$ , $25$ , $30$ . This works with $b_{0} = 30$ .

For $n$ odd (again with $n = c$ ), the condition for collapsing at level $c - 1$ is that:

n! b_{1} \dots b_{n} - \sum_{i = 1}^{n} (b_{0} + b_{i})^{n} + b_{0}^{n} = 0

which rearranges to

n! b_{1} \dots b_{n} + b_{0}^{n} = \sum_{i = 1}^{n} (b_{0} + b_{i})^{n}

Again, note that the case of $n = 3$ is the one we looked at above. As yet, my computer search hasn't found any solutions for $n = 5$ .

At either end of the spectrum of possible collapses, we have similar equations. If a system collapses at level $2$ then Equation 3 becomes:

z^{n} = x_{1}^{n} + \dots + x_{c}^{n}

whereas if a system with $n = c$ and $n$ odd collapses at level $c - 1$ then the collapsing equation is:

n! b_{1} \dots b_{n} + b_{0}^{n} = (b_{0} + b_{1})^{n} + \dots + (b_{0} + b_{n})^{n}

and these are intriguingly similar.

7.4 Marginal Notes

I really ought to end this section with some sort of statement about which systems collapse and a remark along the lines of how I have a marvellous proof of it, but that the internet is not big enough to hold it.

But I won't.

8 Conclusion

This started as a riff off of Ben Orlin's post, but grew somewhat in the telling. That it did so, I think, underlines Ben's point that reformulating a piece of Mathematics can give fresh insight into it.

Being neither a Number Theorist nor a Combinatorialist, I have no idea as to whether what I wrote above is well-known, known but obscure, or new, but that doesn't matter as it was all new to me. It gave me an opportunity to play in an area of Mathematics that I don't often visit. I just hope I didn't make a mess!

I've now said a few times that I'm not a Number Theorist, nor a Combinatorialist. My leaning is to the Topological and Geometrical. With that in mind, to finish this article here's a geometrical reformulation of Fermat's Last Theorem for you.

For $p \geq 2$ , let $∥ \cdot ∥_{p}$ denote the $p$ –norm on $ℝ^{2}$ . That is,

∥ (x, y) ∥_{p} = (x^{p} + y^{p})^{1 / p}

The case $p = 2$ is the usual Euclidean norm. Let $S_{p}^{1}$ be the unit circle with this norm. Then Fermat's Last Theorem is equivalent to the statement that for $p > 2$ :

S_{p}^{1} \cap ℚ^{2} = {(\pm 1, 0), (0, \pm 1)} .

Contents