1 Introduction

I've been aware of the existence of the formula for the solutions of a cubic for a long time. I've never been able to remember it. I've never wanted to use it. (These two statements may not be completely independent.) What is slightly more irksome is that I've never understood it.

Until recently, that is, when a curious conjunction of encounters caused connections in my cerebellum1.

These encounters were:

1. A talk by Deborah Kent about visualising geometry which happened to mention cubic equations as an example, based on this article2.

   2Note that I heard the talk in a context that meant that I wasn't concentrating on the construction, and it was sufficiently long ago that I didn't make the connection to what I was thinking here until after I had thunk it.

2. A puzzle passed on by Ed Southall.

3. A blog post by Benjamin Leis.

Prompted by those, I was able to first figure out a crucial step in deriving the cubic formula and then to come up with a rationale for why that step is the right thing to do.

As per usual on this website, I'm not claiming anything new, just new for me.

Our goal is to solve a general cubic. That is, find solutions of an equation of the form:

$$a{x}^3+b{x}^2+cx+d=0$$

1

2 Depressing a Cubic

The initial steps in solving the cubic in (1) involve turning it into a depressed cubic. This is achieved through a series of transformations.

1. Divide through by $a$ to get:

   $$x^3+b_1{x}^2+c_{1}x+d_1=0$$

2. Apply the transformation $x\mapsto x-\frac{b_1}{3}$ to get:

   $$x^3+c_{2}x+d_2=0$$

3. Apply the transformation $x\mapsto \sqrt{|c_2/3|}x$ to get:

   $$x^3\pm 3x+d_3=0$$

   2

3 Solving Algebraically

To solve the depressed cubic we make a further substitution:

$$x=s+t$$

This substitution leads to:

$$\begin{array}{rl}{x}^3& =(s+t{)}^3\\ & =s^3+3s^{2}t+3s{t}^2+t^3\\ & =s^3+t^3+3st(s+t)\end{array}$$

We're substituting one variable ($x$) for two ($s$ and $t$) so we have the freedom to impose a restriction. The restriction we choose is that $st=\mp 1$ which means that the third term there is $\mp 3x$, so $x^3\pm 3x$ simplifies to $s^3+t^3=s^3\mp s^{-3}$ and the cubic becomes:

$$s^3\mp s^{-3}+d_3=0$$

Multiplying up by $s^3$ gives:

$$s^6+d_3{s}^3\mp 1=0$$

This is a quadratic in $s^3$ and so can be solved using the quadratic formula, whereupon cube rooting those solutions gives solutions to the depressed cubic, and hence to the original cubic.

4 Solving Geometrically

The accumulation of stuff that I'd read, heard, and puzzled through led to me seeing that the substitution $x=s+t$ was the right thing to do. It didn't, however, show me how to have thought of that ex nihilo. That is, knowing to substitute $x=s+t$ I can see how to work through to the solution. But I wouldn't have known to try $x=s+t$ without plenty of hints.

Someone with a more algebraic viewpoint might argue that trying different substitutions is a natural thing to do and that $x=s+t$ is a fairly obvious thing to try. But I'm a geometer so I want a geometric explanation. This is where a half-remembered talk helped me see what was going on.

Let's consider Equation (2) with the minus sign and rearrange it to:

$$x^3=3x+d_4$$

Geometrically, the left-hand side is obviously the volume of a cube of side length $x$. We therefore want to interpret the two terms on the right as volumes. The constant can just be an indeterminate shape of a given volume, but we want to be more careful with the $3x$ term. We'll keep the $3$ as "$3$ lots of …" and make the $x$ represent a cuboid of volume $x$. To make it such, we have one side of length $x$ and two other sides of lengths, say, $s$ and $t$. So that it has total volume $x$ we need $st=1$.

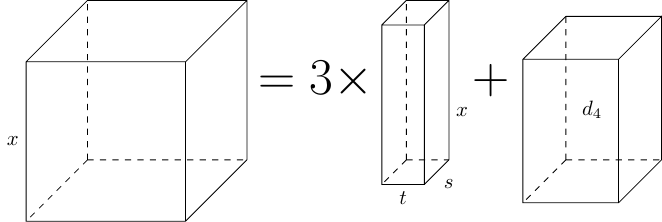
When faced with an equation with the unknown occurring more than once, the natural instinct is to try to put the terms containing the unknown together. In this case, we would try to remove three cuboids from the cube. As one side of our cuboid is length $x$, it makes sense to match this with one of the sides of the cube. So we pick three edges of the cube that don't meet and excise a cuboid from the cube along each edge of the correct volume.

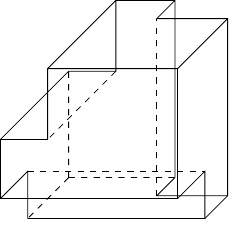
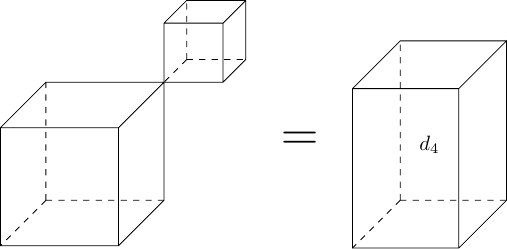
The crucial insight arises when we realise that the simplest shape we can make in doing this is when the slices just touch each other. This means that we want $s+t=x$. We are then left with two cubes cut out from our original one with volumes $s^3$ and $t^3$. So our equation reduces to $s^3+t^3=d_4$.

5 Algebraic Geometry

Now, what happens next is geometrically very interesting. We have $s^3+t^3=d_4$ with $st=1$, meaning that we are trying to find two cubes with a prescribed volume. We apply a scale factor to the resulting diagram so that one of the cubes has side length $1$. This yields $s^6-d_4{s}^3+1$. The $s^6$ here is really a cube of side length $s^2$. So although a term $s^6$ looks like the hyper-volume of a $6$–dimensional object, it is really a $3$–dimensional cube with an interesting scale factor. But now we're going to play a geometrical con trick. Instead of thinking of it as a $3$–dimensional cube with sides of length $s^2$, we're going to think of it as a $2$–dimensional square with sides of length $s^3$. This means that instead of viewing $s^6-d_4{s}^3+1$ as an equation in $s^2$ we view it as an equation in $s^3$.

The point is that I'm not convinced that trying to make an overall geometric picture which encompasses every step is helpful. Rather, I used a series of geometrical pictures to gain insight as to what algebra to do. But then once each insight was gained, the relevant picture is discarded and a new picture (say, that of completing the square) used for the next stage. So although solving cubics (and quadratics) is very geometrical, and even though I am at heart a geometer, it feels very much that algebra is in charge here and the geometry a humble servant.

Well, perhaps not all that humble.