1 Introduction

Titles are always misleading, and this is no exception. This isn't my favourite proof in mathematics – I'm not sure that such exists – it's my favourite proof of Pythagoras' Theorem. And even then I reserve the right to change my mind if I encounter a better one. There are, after all, rather a lot of proofs of Pythagoras. I haven't read them all and so there may well be a better proof lurking down in the depths just waiting for me to encounter it. But if there is, it's going to have to be something really special to beat this one.

I'm going to generalise wildly here. As a young mathematician, you tend to think it's all about the theorems. Proofs explain why you can trust those theorems, but it is the results that you want to use and so the results that you focus on. As you age, you come to appreciate proofs far more. It is no longer the what but the why that matters. A result can be used, that's sure, but a proof can be adapted and mined for deeper understanding. A proof has insight and potential.

And that's what I like about this proof so much. Amongst all the proofs that I've encountered of Pythagoras' theorem it is the one where the properties of the surrounding Euclidean space are the most evident. It therefore offers the most insight as to why Pythagoras' theorem is true (in particular, it is all about length and there is no mention of area). It also has a very simple extension to the generalisation of Pythagoras' theorem, more commonly known as the cosine rule, and within that a demonstration of the fact/definition that $\cos ({180}^{\circ }-C)=-\cos (C)$.

2 Pythagoras' Theorem

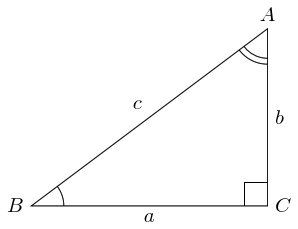
Let's recall the statement of Pythagoras' theorem.

3 The Proof

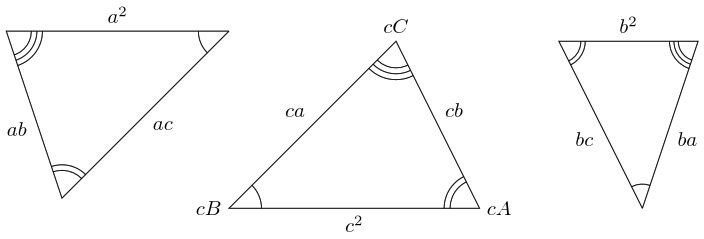
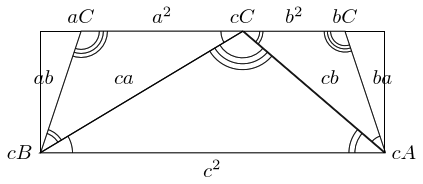
The proof is as follows. Consider three scaled versions of the triangle, one with scale factor $a$, one with $b$, and one with $c$. Let these be ${\Delta }_a$, ${\Delta }_b$, and ${\Delta }_c$ respectively.

As these are scaled versions of the original triangle, the lengths of the sides of each can be found by multiplying the corresponding length from the original triangle by the scale factor. Thus the lengths of ${\Delta }_c$ are $ca$, $cb$, and $c^2$. The hypotenuses of ${\Delta }_a$ and ${\Delta }_b$ are, respectively, $ac$ and $bc$.

These hypotenuses are the same as the non-hypotenuse side lengths of ${\Delta }_c$. We can therefore place ${\Delta }_a$ and ${\Delta }_b$ next to ${\Delta }_c$ so that these sides match up. By turning them over, if necessary, we can align them so that at $C$ the sides that meet have lengths $a^2$ and $b^2$.

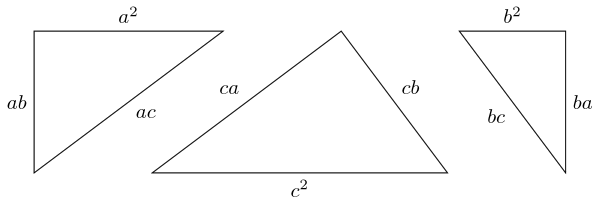
The diagram suggests that when we do this we will obtain a particularly nice shape. This is true, as can be seen by labelling all of the angles.

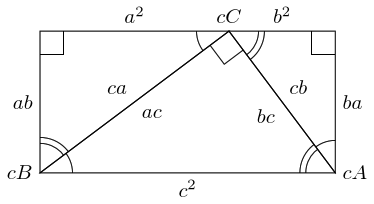
The label "$cB$" means that that point is where point $B$ corresponds to on ${\Delta }_c$.

From this diagram, we can see that the total angle at $cC$ is ${180}^{\circ }$ since the angles are the three angles in the original triangle. Also, the total angles at $cA$ and $cB$ are ${90}^{\circ }$ since these are built from the two non-right angles in the original triangle.

Hence the shape is a rectangle and so the opposite sides are the same length. Thus:

4 The Ingredients of the Proof

Here's the first part of why I like this proof so much: its ingredients. Let's examine what we need to make this work.

1. Lengths scale … as lengths.

   Let's suppose that my original triangle has vertices at $(0,0)$, $(4,0)$, and $(4,3)$. Then when I scale my triangle – by some amount – I mean that I multiply each of those numbers appearing by that amount. So doubling the triangle produces a new one with vertices at $(0,0)$, $(8,0)$, and $(8,6)$.

   The key fact we're using is that if we do this then the lengths of the sides scale by the same amount. In this case, each length also doubles.

   This means that when we scale our original triangle by $a$, $b$, and $c$ then the side lengths of the produced triangles are as we've claimed.

2. Lengths add along straight lines.

   That is to say, the length of the upper side of the rectangle is the sum of the lengths of the two segments.

3. Translation, rotation, and reflection don't change lengths.

   In order to put the triangles together, we've needed to apply some transformations. Whilst we can leave one of them, say ${\Delta }_c$, where it is we need to move, rotate, and flip over the other two. When doing so, we need to know that the lengths of their sides don't change.

   This is also needed to deduce that opposite sides of a rectangle have the same length (translate one side across the rectangle to coincide with its opposite).

4. Translation, rotation, and reflection don't change angles.

   This is used when showing that angles in a triangle add up to ${180}^{\circ }$ and thus that the key line segments which meet at $cC$ join up to make a straight line.

So we have two direct properties of lengths and we combine that with the transformations that preserve geometrical structure.

The fact that this proof concentrates on lengths is what first drew me to it. The vast majority of proofs invoke area. It's easy to see why: what else could $c^2$ be but the area of a square with sides length $c$? But Pythagoras' Theorem is not about areas, it is about lengths. So invoking area to prove it involves introducing a new concept purely for the sake of the proof. If that were essential, then so be it, but the above shows that it is not necessary.

The other half of the foundation consists of the length-preserving transformations. The fact that these transformations preserve length is crucial to so many of the standard geometrical results, but they are rarely mentioned – possibly it is because they are so crucial that familiarity leads to them being overlooked. Indeed, were it not for the fact that we are examining this proof carefully we would probably have overlooked them here.

The theorem is about length, and the proof is about length. The theorem is in the context of Euclidean geometry, and the proof relies on some very basic properties of that geometry.

That's why I like the proof so much.

5 Going Beyond

But there's more.

Let's run the proof again, but without the assumption that the triangle be a right-angled triangle. We'll start with an acute angle at $C$.

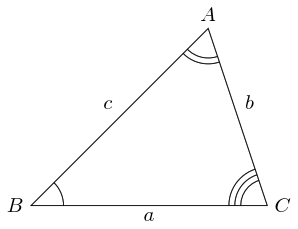
Now we scale, rotate, translate, and shift exactly as before.

And place the pieces exactly as before.

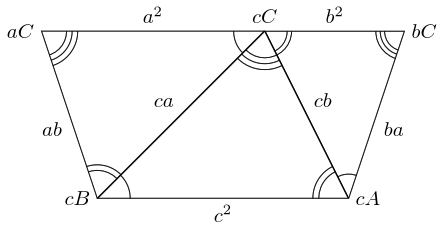
Exactly as before we have a straight line at $cC$, only this time we have a trapezium instead of a rectangle. It is an isosceles trapezium because the interior angles at $aC$ and $bC$ are the same. In fact, both are the angle $C$ from the original triangle.

To compare the lengths of the parallel sides, we drop (or raise) the perpendiculars from $cB$ and $cA$ to the other side.

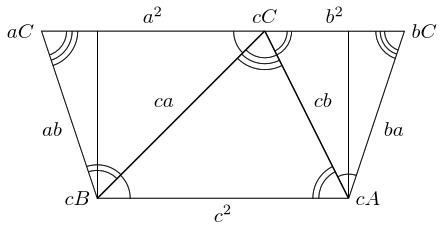
Simple trigonometry says then that the excess on the long side is equal to $ba\cos (bC)$ on the right and $ab\cos (aC)$ on the left. Hence

This was for a triangle with an acute angle at $C$. Now let's run it with an obtuse angle.

All looks fine up to the trapezium, but we find that it is the other way up.

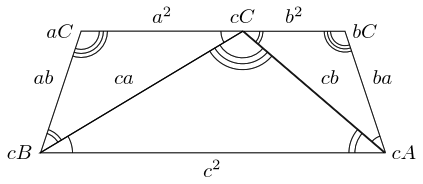
So this time when we drop (or raise) the perpendiculars, we need to add the excess to the $a^2+b^2$ side. The other change is that the angle is now ${180}^{\circ }-C$ since $C$ is the interior angle.

Hence:

Whereupon if we define $\cos$ for obtuse angles via:

then we have the same identity as before:

So this proof of Pythagoras' Theorem extends to prove the more general cosine rule and gives us a reason as to why we define the cosine of an obtuse angle in the way that we do.

6 Conclusion

Context is everything. The proof presented here is not the proof that I would turn to if I needed reassuring that Pythagoras' Theorem were true. None of the proofs that I've encountered to date on Cut The Knot fit that bill (though I've not read the whole lot as yet).

For me, Pythagoras is a simple deduction from the structure of space. But to make that structure precise requires a few concepts that are usually presented several years after students typically first meet Pythagoras. So the proof that I would use wouldn't be suitable for such a first meeting.

The proof that I would use basically says "Euclidean space is a good model for the space around us on the scales that we typically encounter1, and Pythagoras' theorem holds in Euclidean space.". The key there is the first part: that Euclidean space (whatever that is) is a good model for the space around us. One way to show that is to observe that length and angle behave in a certain way under certain transformations, such as rotation, translation, reflection, and scaling.

Thus while this proof of Pythagoras' Theorem is completely elementary, it hints at the true proof. It hints that the key is in the transformations and the structure of the space around you. It hints that Pythagoras is inevitable once you have a good notion of angles. It says that Pythagoras' Theorem is a simple deduction once you realise that my protractor measures angles just the same as yours, even though mine is over here and yours over there, mine is a different size to yours, and is upside-down and turned around. Still, we both agree on the angles we measure. Once we see that, Pythagoras is a simple logical step away.

So it's my favourite proof because it exposes the core of Pythagoras' Theorem in a way that gives more as you understand more. It is like the "magic pool": safe for a baby to paddle in yet an elephant can drown in it. I could present this to students first encountering Pythagoras knowing that there's nothing here they couldn't cope with. Yet I can also use it as a springboard for advanced students that will lead them deep into real geometry.

Little wonder I like it so much.

7 Postscript

As a little extra, here's a Geogebra Worksheet that demonstrates this construction.