1 Introduction

I was playing around with formulae involving rectangles and figured out a different take on the geometry of completing the square. My aim was to create an activity with the various formulae relating the width and height of a rectangle to its perimeter and area. Obviously, starting with the width and height then one can easily calculate the perimeter and width, but going the other way involves solving a quadratic. The level at which I was aiming this activity meant that I didn't want to make that explicit, but wondered if I could figure out how to make solving it a natural progression.

2 The Quadratic Equation

The quadratic equation for the width is simple to set up. The equations linking area, $A$, perimeter, $P$, height, $h$, and width, $w$, are:

$$\begin{array}{rl}A& =wh,\\ P& =2w+2h.\end{array}$$

So if we know $A$ and $P$, we can get an equation for $w$ by eliminating $h$:

$$\begin{array}{rl}h& =\frac{A}{w},\\ P& =2w+\frac{2A}{w}.\end{array}$$

Multiplying up and rearranging yields:

$$w^2-\frac{P}{2}w+A=0.$$

Completing the square on this produces:

$$(w-\frac{P}{4}{)}^2=\frac{P^2}{16}-A$$

1

The goal is to find a way to effectively get that formula without doing the algebra or mentioning the phrase "quadratic equation".

3 Finding the Square

Key to Equation (1) is the quantity $\frac{P}{4}$. So to find a route to Equation (1), we need to find a justification for the quantity $\frac{P}{4}$.

This is quite straightforward to come up with since the quantity $P$ is the perimeter of a rectangle. If it were the perimeter of a square then $\frac{P}{4}$ would be the side length. So $\frac{P}{4}$ is the side length of a square with the same perimeter as our original rectangle.

Looking at Equation (1), the quantity $\frac{P^2}{16}$ is then the area of that square and $\frac{P^2}{16}-A$ is the difference between the area of the square and the original rectangle.

If we then tried to solve for $w$, we would square root $\frac{P^2}{16}-A$. Geometrically, this again means finding a square but this time with area $\frac{P^2}{16}-A$.

So the pieces we have are:

• A square with the same perimeter as the original rectangle,

• A second square whose area is the difference between the new square and the original rectangle.

We want to put those together in a way that makes the story clear.

4 Completing the Square Geometrically

The obvious thing to do is to draw the squares. The first square is straightforward.

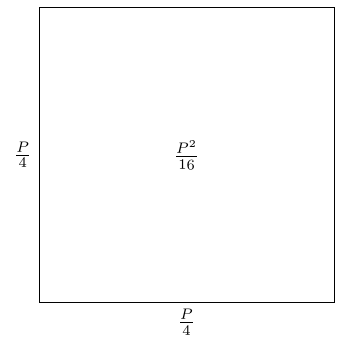
The second square has area the difference between this and the rectangle. We model differences by subtraction, so we can subtract the second square from the first.

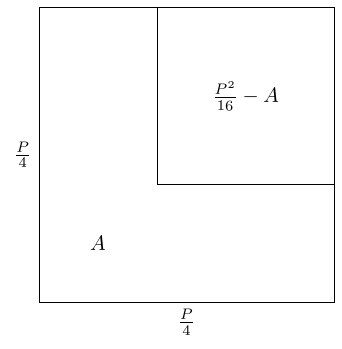
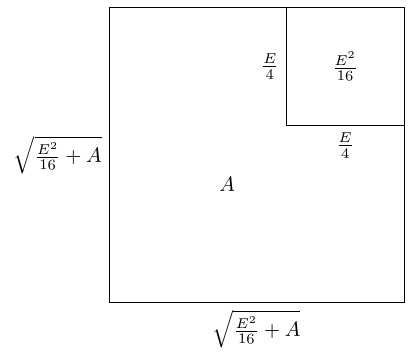
As the smaller square has area $\frac{P^2}{16}-A$ and the larger square area $\frac{P^2}{16}$, what is left over has area $A$. This means that the left over region has area $A$ and, as we've drawn it, perimeter $P$.

So that region is almost what we want: it has area $A$ and perimeter $P$. Unfortunately, it's not a rectangle. Fortunately, rearranging it into a rectangle doesn't change either the area or the perimeter because the two green line segments are the same length.

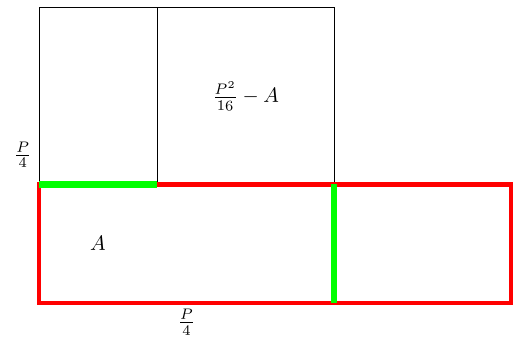
The red rectangle is what we're after: it has perimeter $P$ and area $A$.

The picture makes clear that its width and height are the sum and difference of the sides of the two squares:

$$\begin{array}{rl}w& =\frac{P}{4}+\sqrt{\frac{P^2}{16}-A},\\ h& =\frac{P}{4}-\sqrt{\frac{P^2}{16}-A}.\end{array}$$

5 Hiding the Details

In the previous section, we worked from Equation (1) to a geometric picture. We can run that in reverse. Let's start with actual numbers. Consider a rectangle with perimeter $48$ and area $135$.

We want a rectangle with these details. Let's focus on the perimeter, and look at rectangles with perimeter $48$. The simplest such would be a square, and to get a square with perimeter $48$ we need a side length of $12$.

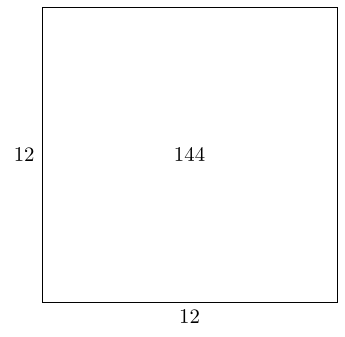
This has an area of $144$ which is $144-135=9$ too much. So we want to remove an area of $9$ from this square, which we can do by removing a square of side length $\sqrt{9}=3$.

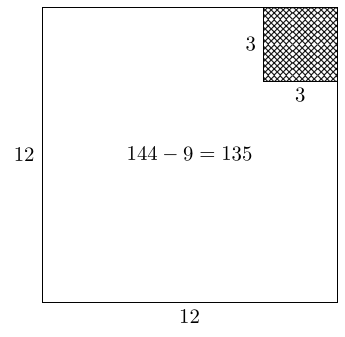
Finally, rearrange the remaining shape into a rectangle.

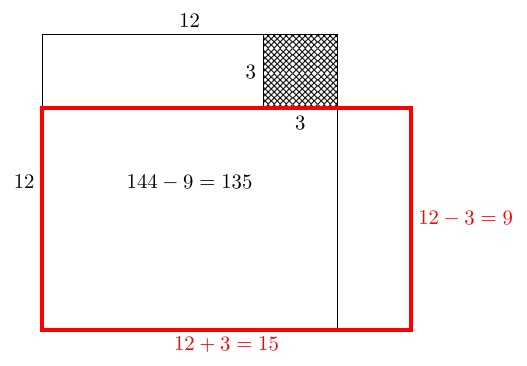
We can run this algorithm from an arbitrary starting point, i.e., perimeter $P$ and area $A$. To get a square with perimeter $P$ we need side length $\frac{P}{4}$. This square has area $\frac{P^2}{16}$, which is $\frac{P^2}{16}-A$ too much. So we remove a square of side length $\sqrt{\frac{P^2}{16}-A}$ to make a (symmetric) $L$–shape. This has perimeter $P$ and area $A$ and can be rearranged into a rectangle without changing its perimeter or area. The final dimensions of this rectangle are:

$$\begin{array}{rl}w& =\frac{P}{4}+\sqrt{\frac{P^2}{16}-A},\\ h& =\frac{P}{4}-\sqrt{\frac{P^2}{16}-A}.\end{array}$$

6 Negatives

The above strategy can be used to solve a quadratic of the form: $x^2-bx+c=0$ with $b$ and $c$ positive. If we start instead with $x^2+bx+c$ then this is like having a rectangle with both width and height negative. This simply means that the ruler was the wrong way around. However, one of the form $x^2-bx-c$ is a little more complicated.

To get a quadratic of the form $x^2-bx-c$ we need the roots to be of opposite signs. Then with $(x-\alpha )(x+\beta )=x^2-bx-c$ we have that $\alpha -\beta =b$ and $\alpha \beta =c$. So to solve this type of quadratic, the $x$–coefficient wouldn't be the perimeter of a rectangle but would be related to the difference in the lengths.

With that as our guide, let's define the excess perimeter, $E$, of a rectangle to be the perimeter of the rectangle minus the perimeter of the largest included square. For definiteness, let us suppose that our rectangle is wider than it is high, so then the perimeter of the largest included square is $4h$ and the excess perimeter is thus:

$$E=P-4h=2w+2h-4h=2w-2h$$

Eliminating $h$ results in the quadratic

$$w^2-\frac{E}{2}w-A=0$$

and completing the square produces:

$$(w-\frac{E}{4}{)}^2=\frac{E^2}{16}+A$$

Comparing this with Equation (1) and the construction that followed, we build squares, one of side length $\frac{E}{4}$ and another of area $\frac{E^2}{16}+A$.

The justification for the first square in Section 4 was that of making a square with the same perimeter as our sought-for rectangle. In this case, it is a little harder to explain why we would make a square of side length $\frac{E}{4}$ as $E$ is the excess perimeter. At the simplest level, we can argue that since making a square worked in the first situation, it's worth trying again in this one. Looking a little more carefully at the earlier construction, when we make the rectangle from the $L$–shape then the inner length of the $L$ is half the excess perimeter.

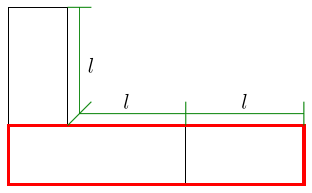
Therefore we want to draw an $L$–shape with inner length $\frac{E}{4}$ and we can start by drawing a square of side length $\frac{E}{4}$ to be the inside of the $L$.

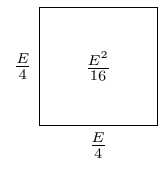
The $L$ should have area $A$, and so the full square should have area $A$ plus the area of the inner square. That is, $\frac{E^2}{16}+A$. Thus the side lengths of this square are $\sqrt{\frac{E^2}{16}+A}$.

Making this $L$–shape into a rectangle gives us the rectangle we're looking for.

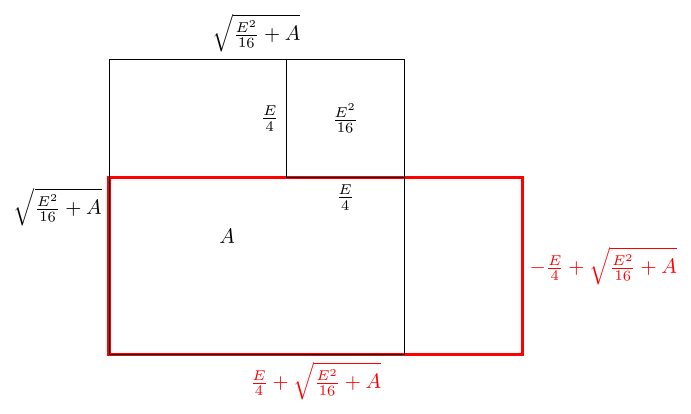
Putting this together, we get a rectangle with dimensions:

$$\begin{array}{rl}w& =\frac{E}{4}+\sqrt{\frac{E^2}{16}+A},\\ h& =-\frac{E}{4}+\sqrt{\frac{E^2}{16}+A},\end{array}$$

and we observe that

$$2w-2h=2(\frac{E}{4}+\sqrt{\frac{E^2}{16}+A})-2(-\frac{E}{4}+\sqrt{\frac{E^2}{16}+A})=E.$$

One noticeable difference between the situation here and the previous one is that the two solutions of this quadratic are not the values of $w$ and $h$. This makes sense since we assumed at the outset that the width was bigger than the height. The other solution to the quadratic corresponds to a rectangle with width $-h$ and height $-w$, noting that both of these are negative and so again we had the ruler the wrong way around.

7 Conclusion

There are several things I like about this approach, particularly the initial method with the perimeter.

1. It can be done without mentioning quadratics at all.

   This may seem a bit of a bizarre thing to note, but the idea originally came about because I was designing an activity aimed at students who won't have met quadratics. It's more about manipulating formulae and expressions. But by using quadratics underneath, it will link to that topic when it is introduced.

2. It shows why there can be two, one, or no solutions.

   The two solutions come from drawing the rectangle in both orientations. We get one solution when the original rectangle was a square (in which case the algorithm terminates early). No solutions might need a bit of explanation as to the fact that a square is the largest rectangle with a given perimeter, but so long as the students are happy with that then we see that if $\frac{P^2}{16}$ is less than $A$, we can't make a rectangle with area $A$ as $\frac{P^2}{16}$ is the maximum size.

3. The squares appear naturally.

   The usual picture version of "completing the square" involves trying to build a square out of some pieces with areas, say, an $x^2$, $4$ lots of $x$, and $3$ units. But why should one want to make a square out of those pieces? And why do they have the shape that they do? Here, it feels, the squares are linked directly to the problem: right from the outset we're trying to build a shape.

4. The divisions appear naturally.

   One thing my students find tricky with completing the square is why we halve the coefficient of $x$. "Because it works" is, at present, my best response. Here, though, the division makes sense. To get a square with perimeter $P$ we need side length $\frac{P}{4}$1.

5. It leads on to quadratics.

   If we're trying to solve $(x-\alpha )(x-\beta )=x^2+bx+c$ then we're looking for $\alpha$ and $\beta$ such that $\alpha +\beta =-b$ and $\alpha \beta =c$. Taking $\alpha$ and $\beta$ as the sides of a rectangle, it has area $c$ and perimeter $-2b$. Hence its solutions are:

   $$\begin{array}{rl}\alpha & =\frac{-2b}{4}+\sqrt{\frac{(-2b{)}^2}{16}-c}=-\frac{b}{2}+\sqrt{\frac{b}{4}-c},\\ \beta & =\frac{-2b}{4}-\sqrt{\frac{(-2b{)}^2}{16}-c}=-\frac{b}{2}-\sqrt{\frac{b}{4}-c}.\end{array}$$