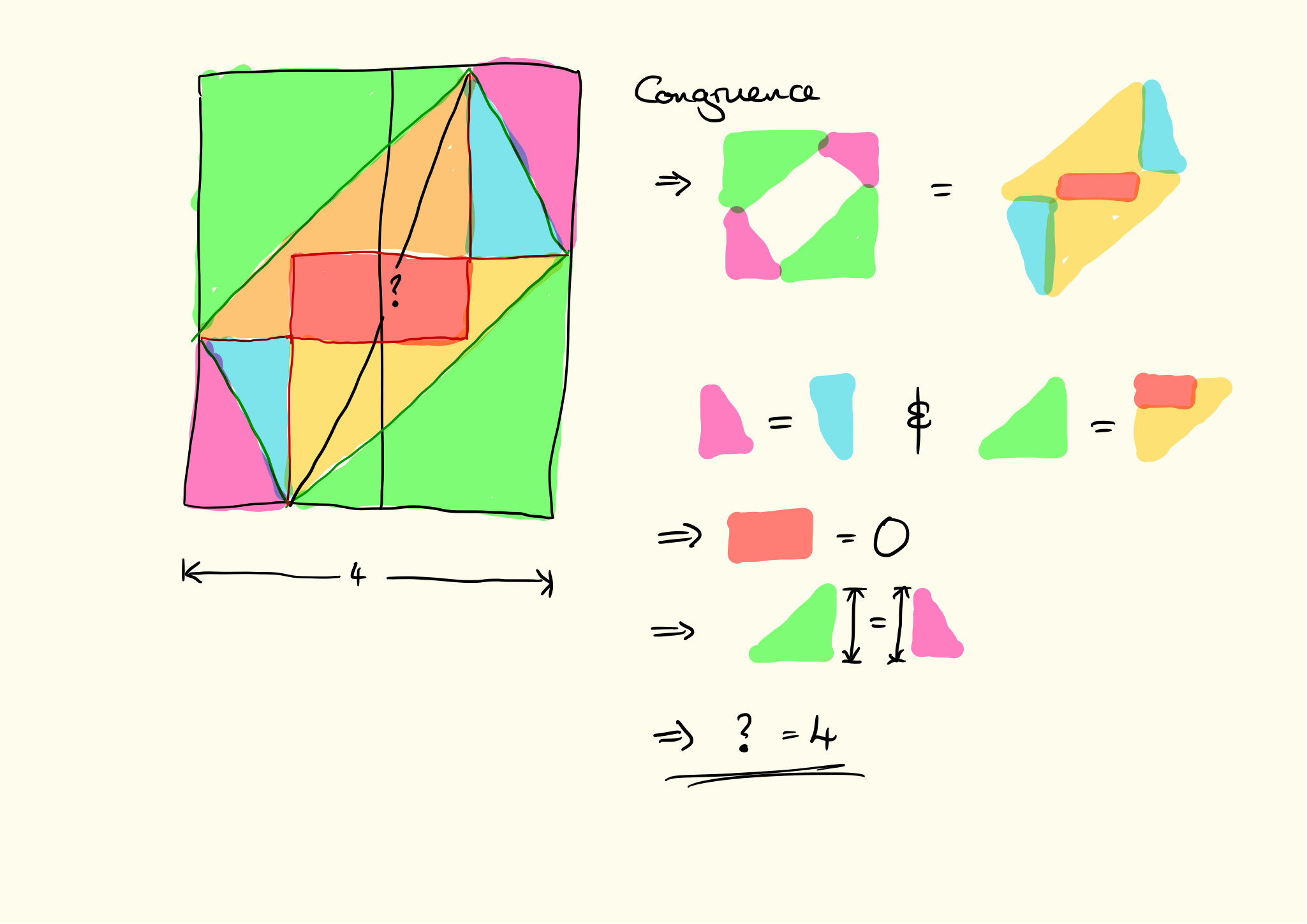1 Introduction

One thing that Mathematics does very well is compartmentalising. We gather together concepts into a single definition which we can then cart around without having to think of the original distinct ideas. We can work with a square without having to always be thinking "a four-sided polygon with all four sides the same length and all interior angles the same". A similar thing happens with theorems. We can say that angles in the same segment are equal without having to remember "because there are a lot of isosceles triangles about". Once a thing is proven, we don't have to keep reproving it every time we use it.

But while compartmentalising is an extremely powerful technique, it can be a little confusing to be just handed the concept or result with no idea how it got into its box. It is like seeing some marvel of architecture and wondering how it got put up, and who would have thought to construct it as it is. With that analogy in mind, it can sometimes be useful to put back the scaffolding so that we can see how it was made and what supports were in place which led to its being built in that particular way.

Problems and puzzles have the same issue. They can often seem to spring full-formed from Zeus' head. It is not so much the internal motivation that is lacking, but rather the answer to the perpetual "How did someone come up with that?", which can be asked both of the puzzle and its solution.

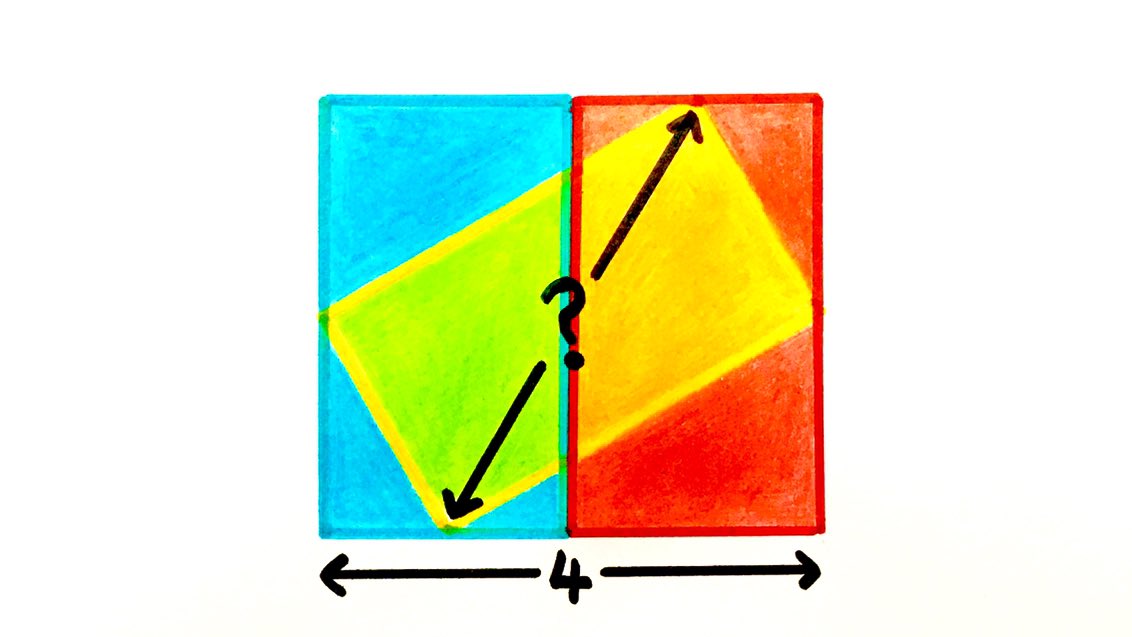
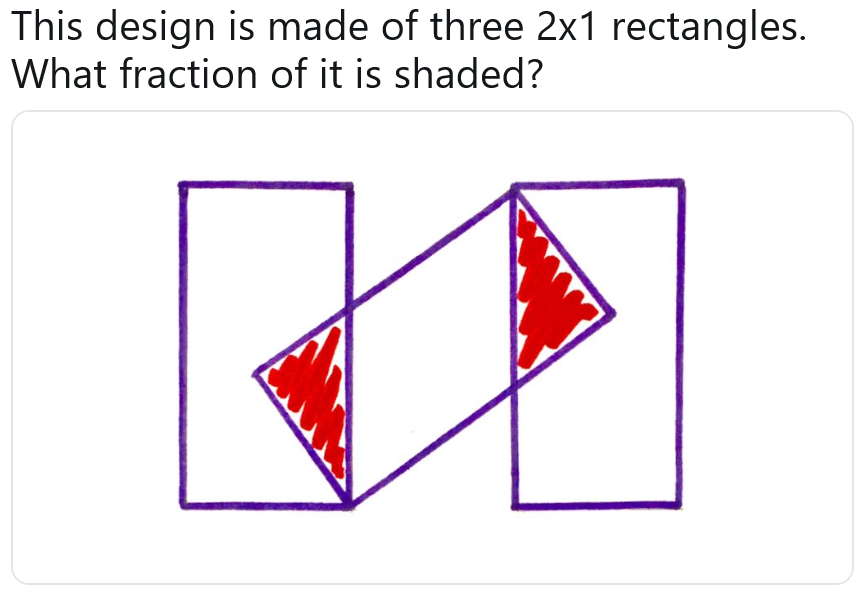
What we want to do here, then, is put back the scaffolding. We thought it would be insightful to see both how a puzzle was conceived and then how it was solved. The puzzle setter is Catriona Shearer and the solver is loopspace. The puzzle in question is this one, which can also be found on twitter, in which all three rectangles are congruent.

We'll start with Catriona's account of how this particular puzzle came into being.

2 Constructing the Puzzle, by Catriona Shearer

2.1 The Source

A few months ago I made the following puzzle.

One of the things I liked about this construction is that the space between the rectangles is the same width as the rectangles themselves. You could imagine the design actually being made of four congruent rectangles: three touching side-by-side, and a fourth lying diagonally across the middle.

Cycling home one evening last week, I started wondering about a similar diagram, but where all four corners of the fourth rectangle reached the sides. I was imagining a French flag with a yellow rectangle lying over the top, which would create some orange and green sections – I got a bit carried away visualising this colour scheme. The maths was proving a lot harder to do in my head. Clearly the $2\times 1$ rectangles in the original diagram wouldn't work – the diagonal rectangle just isn't long enough to reach all the way across. What dimensions would the rectangles need to have to make it possible?

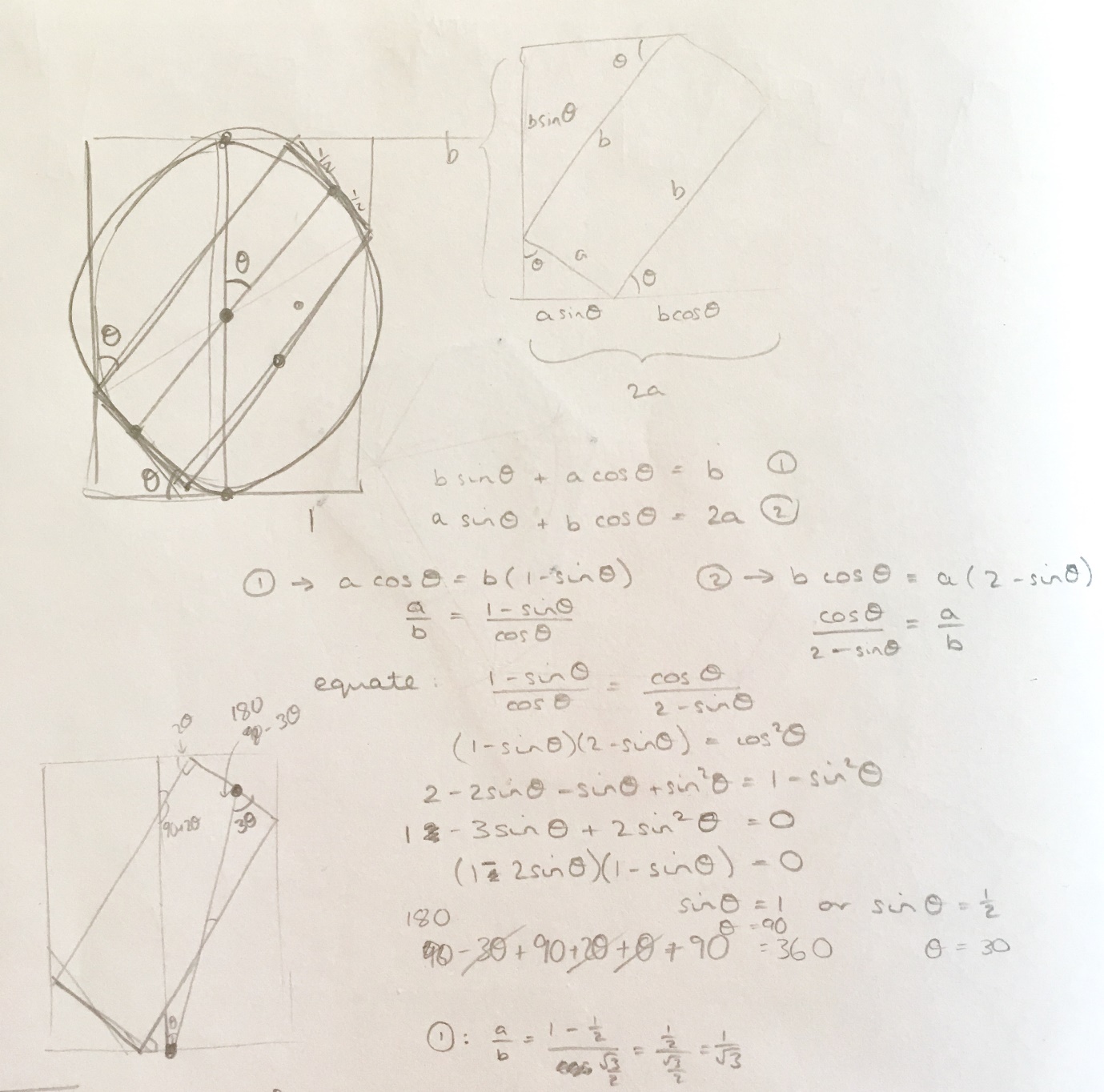
Back at home, I tried to draw the image that was swimming around in my head. I had no idea what size the rectangles would need to be, and I had a hunch it wasn't going to be a "nice" integer ratio that would fit neatly onto my squared paper – so I didn't worry too much about the obviously bad scale at this point. The first things that jumped out were lots of similar right-angled triangles, so I tried to use these to come up with some equations to relate the side lengths. My initial working is shown below.

After about 20 minutes it was clear I wasn't getting anywhere. This was frustrating, because it felt like a problem that should have a solution! As a teacher, I know the importance of having a growth mindset, and I also know that I generally fail to exhibit one. So I gave up.

2.2 The Trigonometry

The next day I picked up my pencil again for another go. I realised there was an approach I hadn't tried yet: trigonometry (always my last resort). Things were looking up as I managed to form equations I could actually solve, and better yet a nice answer fell out – the angle of rotation was 90 degrees! A very brief feeling of elation quickly ebbed away as I tried to substitute this back into my equations for the rectangle, and found both sides were equal to zero. Worse still, I couldn't easily spot the mistake in my algebra.

At this point I decided to simplify the problem a bit by only having two rectangles side-by-side, with a third overlapping. I tried doing something clever with circles, which came to nothing. However, when I tried my trigonometric approach again, I was able to get an answer – and better still, a nice one. For two rectangles, the angle of rotation was $30$ degrees, which meant the rectangles must have sides in the ratio $1:\sqrt{3}$.

2.3 The Puzzle

Now I knew the solution for two rectangles, I tried to find a more general case. It turns out there wasn't one! I had some mixed feelings here – I was disappointed that my French flag was never going to be a reality, and a bit embarrassed that I had spent so long looking for a rectangle that didn't exist! On the other hand, it was satisfying to know the solution was unique. At least I wouldn't have to make any decisions about which version of the puzzle to draw up – there was only one option.

I did have to work out how to turn this into a puzzle with a nice answer, though. I've developed a self-imposed rule that answers to my puzzles should be integers, or simple-looking fractions, if at all possible. The ratio of $1:\sqrt{3}$ immediately put me in mind of equilateral triangles, but I couldn't see how to work that in. I settled on asking for the diagonal of the rectangle, which would be double the shorter side length, or equal to the total width of the figure.

3 Solving the Puzzle, by loopspace

3.1 Proofs Without Words

As Catriona's puzzles are so visual, when I solve one I look for a so-called Proof Without Words solution. In a discussion on twitter about solving Catriona's puzzles, someone made the remark:

Gawp slack-jawed in admiration at the beautiful and simple geometrical proof someone else posted that makes your detailed algebra look ugly.

Part of the point of this article is to show that the "beautiful and simple geometrical proof" came from "[ugly] detailed algebra" and that without the algebra, the geometry wouldn't exist.

Proofs without words are a common type of proof that seem to have a special place in people's perceptions. Many regard them as canonical proofs from the book. While a good proof without words can indeed be a thing of beauty, there are two serious pitfalls that a creator of such must be ware of:

1. What is obvious to one might not be obvious to all.

   A proof without words should be a picture that makes the result obviously true. As no words are needed, all the argument should be contained within the picture. But an over-complicated picture rarely makes anything obvious, so there is a tendency towards minimalist pictures. Unfortunately, this can mean that key properties are not always clear. And what is clear to the person who devised the proof may not be clear to the person encountering it solely through the picture.

2. A picture may not be as accurate as it seems.

   There are many classic fake proofs by picture, the proof that all triangles are isosceles being one that springs to mind. A picture can disguise a key element, or imply something that isn't actually true, and so mislead. One of the problems with proof without words is that there is often no direction as to how the flow of the proof should go. Sadly, but not unsurprisingly, the literature – and now the internet – is full of not-quite-proofs which seem plausible but which don't hold up to scrutiny.

   On the plus side, much progress in Mathematics has been made by people looking carefully at seemingly plausible proofs and figuring out what's really going on.

There is then a third issue which is not a pitfall of the method of proof, but rather a consequence of its use. This is that by its nature, a proof without words tends to not have any indication of where it came from. Thus when seeing a proof without words, while one reaction is to go "Wow! It's obvious now!", a second reaction is "I could never think of that.".

And that's the point of this article. To show where a proof without words comes from.

3.2 The Ugly Algebra

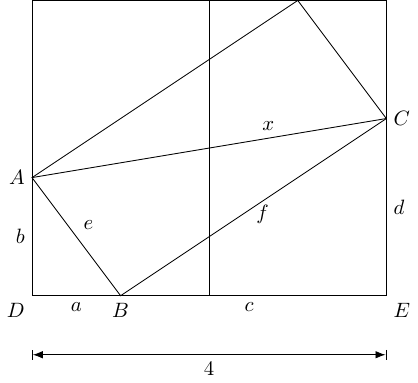
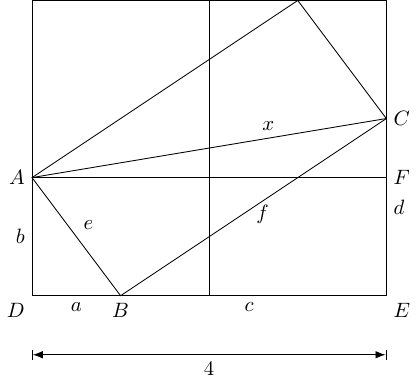
Whether you regard algebra as beautiful or ugly, it is a good place to start with any problem. My initial instinct with a problem such as this is to label everything in sight.

I'm not sure why I flipped the diagonal on the slanted rectangle so that I was looking for the other diagonal, perhaps because the known length was along the bottom and therefore it was more natural to look at near horizontal lengths rather than near vertical.

The next step is to write down all the obvious facts. Clearly, the most obvious is that $a+c=4$. As the rectangles are congruent, we have $e=2$. Then the rotational symmetry of the picture means that the height of the rectangles is $d+b$, and so $f=d+b$.

I have a tendency to look at triangles, so the next thing I spotted was that the triangles $ADB$ and $BEC$ are similar (with that ordering of vertices). This means that:

$$\frac{a}{b}=\frac{d}{c}$$

and so multiplying up gives $ac=db$.

There are lots of right-angled triangles and so lots of opportunities for Pythagoras:

$$\begin{array}{rl}{e}^2& =a^2+b^2\\ f^2& =d^2+c^2\\ x^2& =f^2+e^2\end{array}$$

Combining these gives:

$$x^2=a^2+b^2+c^2+d^2$$

I stared at this for quite some time hoping for inspiration, but sadly none struck.

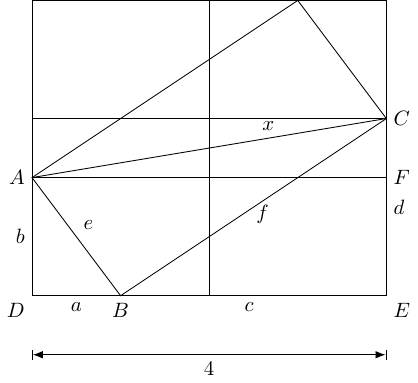
My next idea was to add a horizontal line from $A$ to create a new right-angled triangle.

The rotational symmetry of the diagram means that the distance between $C$ and $F$ is $d-b$. So we have a new identity:

$$x^2=(d-b{)}^2+4^2$$

Using $f=b+d$ and $e=2$, we also have:

$$x^2=(d+b{)}^2+2^2$$

Looking at these together, we have:

$$\begin{array}{rl}{x}^2& =(d-b{)}^2+4^2=d^2+b^2-2bd+16\\ x^2& =(d+b{)}^2+2^2=d^2+b^2+2bd+4\end{array}$$

Subtracting these gives

$$12-4bd=0$$

and so $bd=3$.

We therefore have $ac=bd=3$ and $a+c=4$. The solution to this is $a=1$ and $c=3$ (as $a<c$ it must be this way around).

(In full confessional mode, I feel I should admit to making a mistake when I first tried this. When expanding the brackets I forgot the coefficient of $2$ and ended up with $ac=6$ which has no solutions. I therefore spent some time trying to see why the diagram was actually impossible. Fortunately, I had to run an errand shortly after making this mistake and by the time I returned to the calculation I'd decided that the sensible thing was to redo it whereupon I did it correctly.)

It is worth pointing out here that although the values of $a$ and $c$ were easy to spot, in effect I was solving a quadratic equation so if Catriona hadn't chosen nice numbers I could have been wielding the quadratic formula at this point. That's how "ugly" the algebra gets.

As this is an account of a process, I will also confess to it taking me longer than I'd care to admit to to compute $b$ and $d$. We get $b$ from Pythagoras since $e=2$:

$$b^2=e^2-a^2=4-1=3$$

so $b=\sqrt{3}$. Then since $bd=3$, we get that $d=\sqrt{3}$ also.

The Big Conclusion is thus that $b=d$ and hence that the line from $A$ to $C$ is horizontal, whence $x=4$.

Crucial to what comes next is that the key was establishing that $b=d$. The rest followed from that.

3.3 The Big Picture

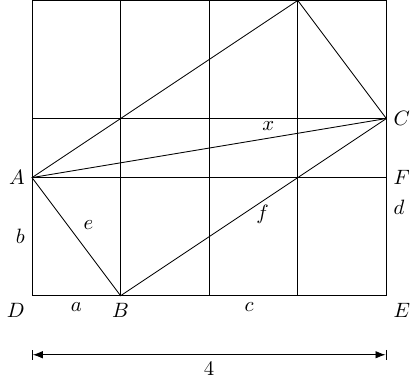
Knowing that the goal is $b=d$, the first thing to do is to add horizontal lines at height $b$ and $d$ as in Figure 8.

I'm always on the look out for triangles, so it's quite natural to flip triangle $ADB$ along its hypotenuse, and $CEB$ along its. This results in vertical lines at $B$ and where the slanted rectangle meets the top.

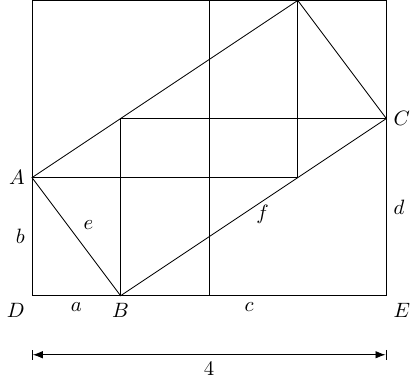
Now, the goal is to show that the horizontal lines are actually the same. Experience with Catriona's puzzles leads me to look for areas, so the central rectangle does rather leap out. Focussing on that rectangle, we can reduce the number of lines a little to help see the structure in Figure 10.

At this point, the final proof without words, in Figure 11, is in place.

3.4 Cheating

The proof without words is actually a cheat. It is only "without words" because I've used pictures in place of symbols, but there are actually several lines of explanation. It is also not fully accurate: for a general set of rectangles, there's no reason why the larger triangle should fit wholly within the slanted rectangle. The argument can be readily adapted (it makes an equality an inequality, but the argument stays fundamentally the same) but it does lessen the elegance.

And, as with most proofs without words, it has no scaffolding. That lack we can, at least, remedy. And if you've made it this far, we hope that you have seen where that scaffolding was and can appreciate better how it was put together.