1 Introduction (Andrew)

Catriona has been taking a break from puzzle setting of late and while there's a considerable back catalogue to keep puzzling with, it was a nice surprise to read a tweet1 teasing a possible new puzzle.

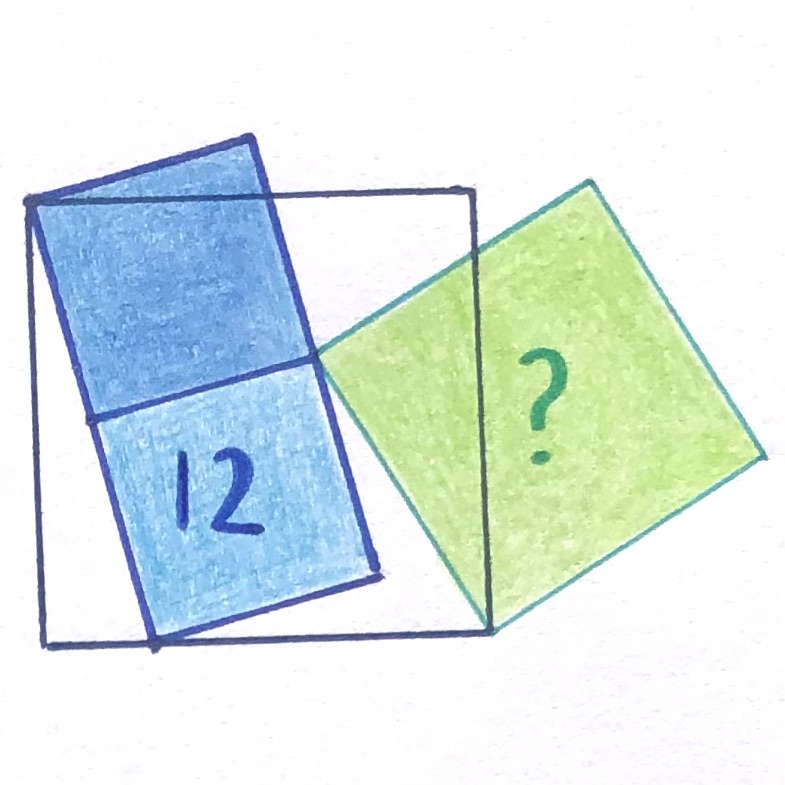
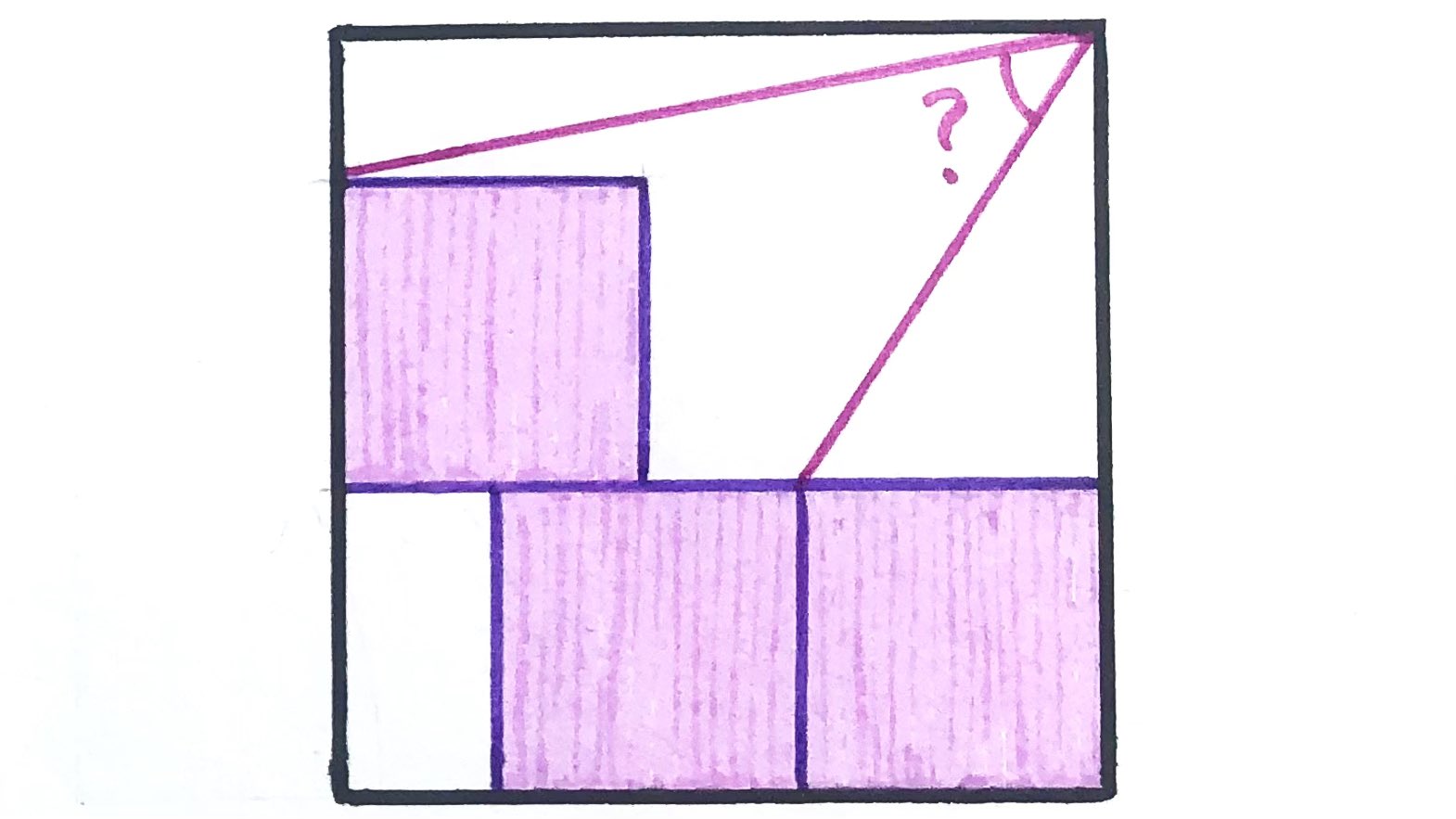
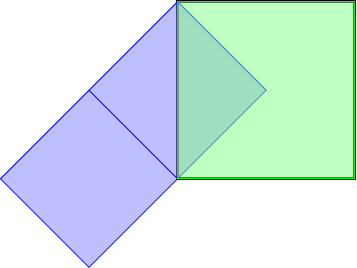
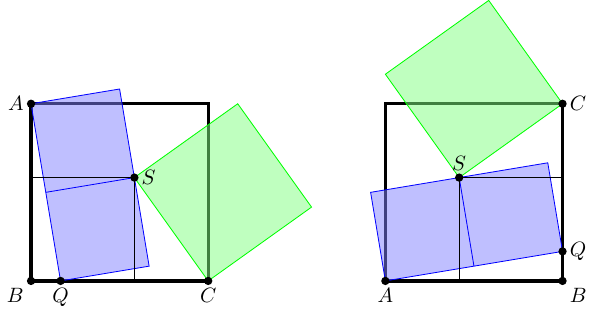
Sure enough, a few days later Catriona posted the image in Figure 1.

The story behind it is curious: as Catriona explained this was a puzzle that she'd created some time previously and so there was something of a mystery as to why she hadn't posted it at the time. Was it actually a puzzle? Or was it something she'd tried to make into a puzzle but which ultimately hadn't worked? So for this one, she'd had to work backwards from the diagram.

This felt to me sufficiently unusual that I thought it would be interesting to hear what that experience was like for her. I must've caught her on a good day as it didn't take much persuading to get the story.

After her account of creating the puzzle, I'll turn to solving it. It turns out to be an excellent puzzle for show-casing the Agg Invariance Principle.

2 The Tale of the Puzzle (Catriona)

2.1 Discovery

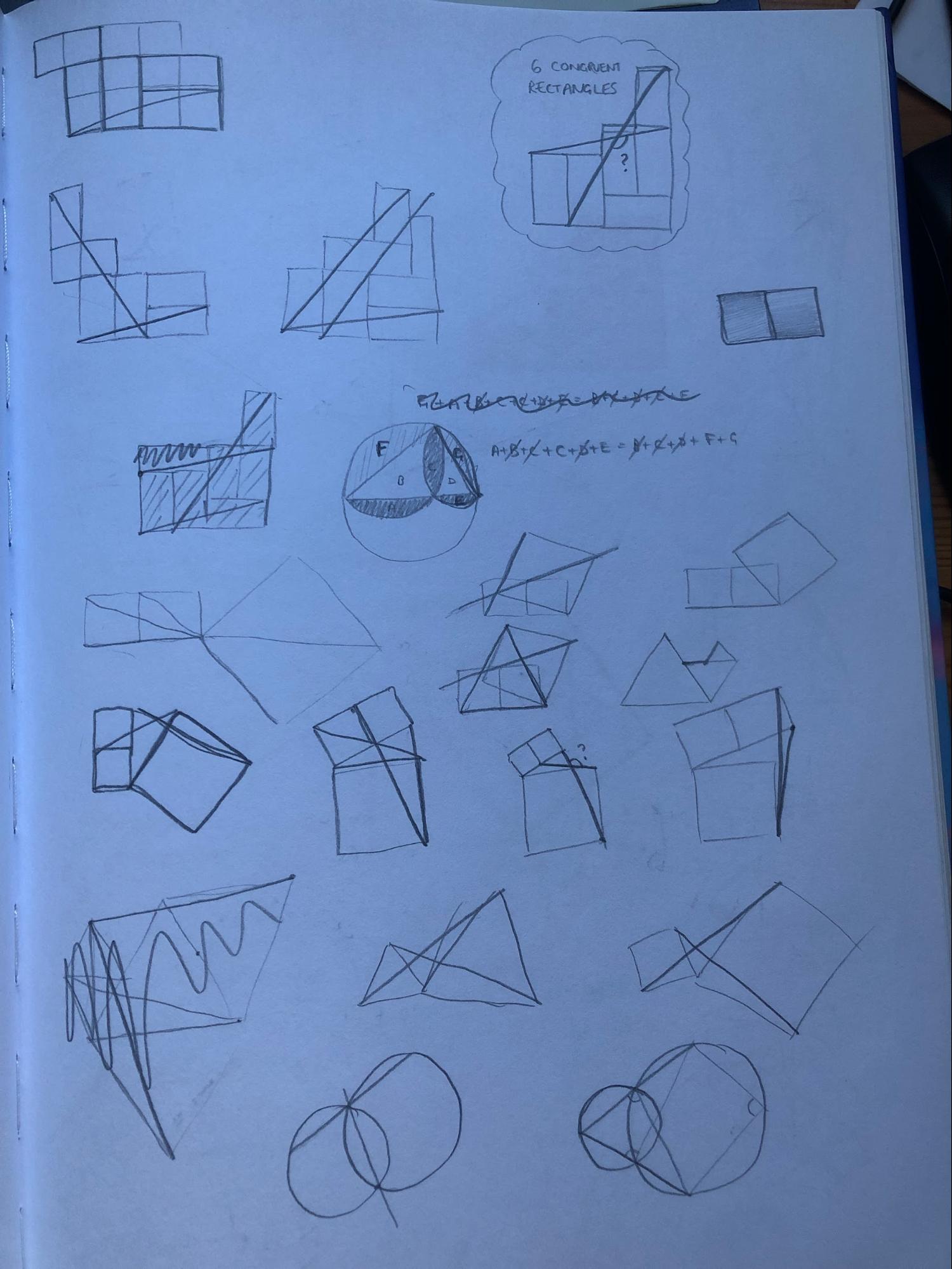
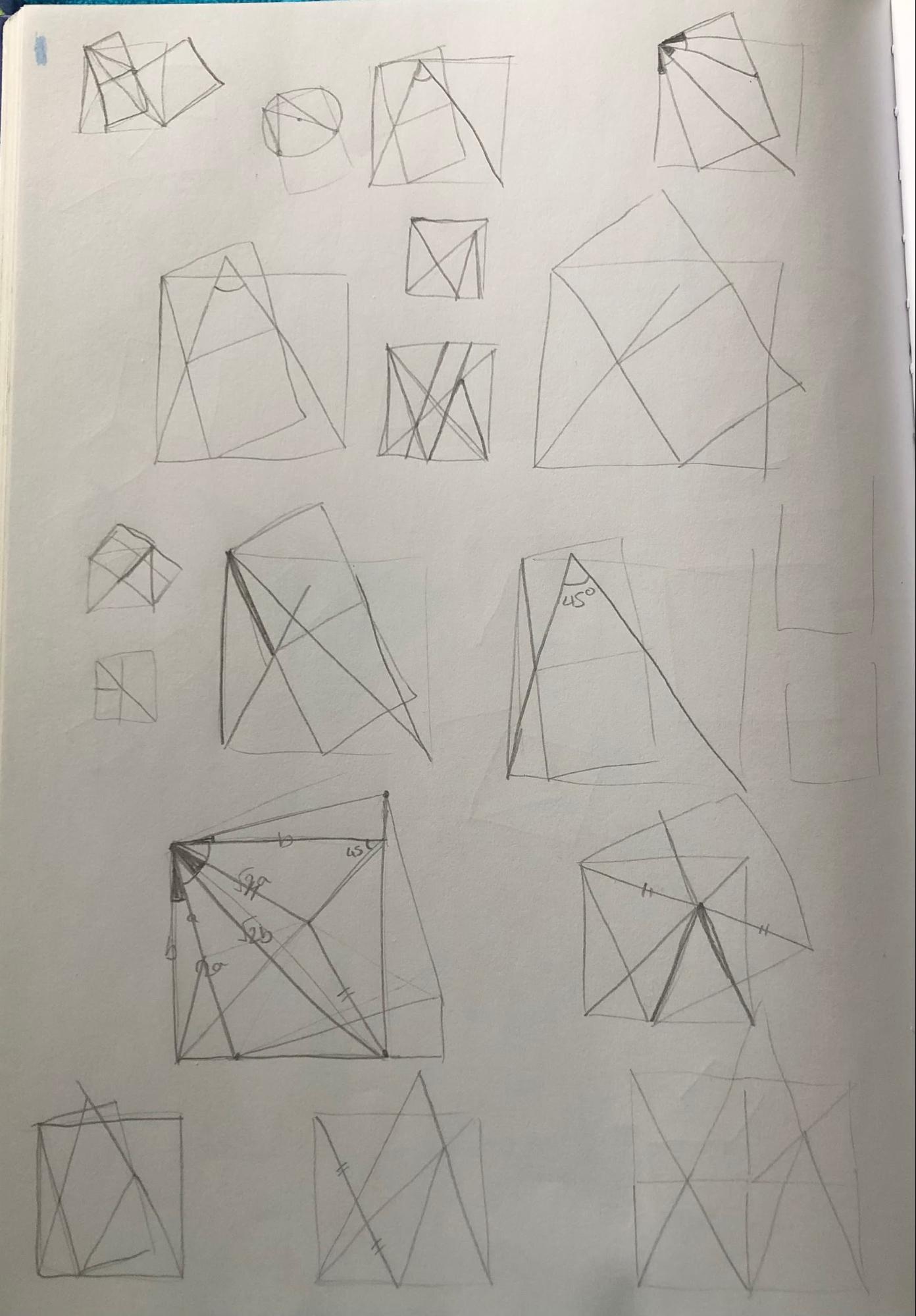
I had a long break from puzzle-making over the winter. So it was a big surprise to open up my notebook for the first time in months and find that on the final page was a fully coloured-in puzzle, which I'd apparently never posted anywhere.

It's not uncommon for my notebook to have sketches of puzzles which I haven't published. Usually this is because two similar ideas occur to me at the same time, so I'll choose one to draw neatly and photograph, leaving the other ready to be found later. Here's an example from where I left myself a puzzle to find at the top of the page, and later in the book I've drawn it out properly.

It's rare that I would go to the trouble of drawing one out and then not photograph it though (after all, drawing them neatly is often the hard bit!). I had to do a quick search through my emails and twitter messages to check that I hadn't made this one for some non-public purpose that I'd since forgotten about. But there wasn't even a picture on my phone's camera roll, which means I hadn't sent it to anyone.

This left two options: either I'd forgotten about the puzzle after drawing it – perhaps I'd just seen someone else publish a similar one so decided to hold on for a few days – or I'd realised there was a mistake in it. When I found the puzzle, it didn't have the blue 12 or green ? drawn on, so even if there wasn't a mistake, I'd need to reverse engineer the question to go with it.

2.2 Origins

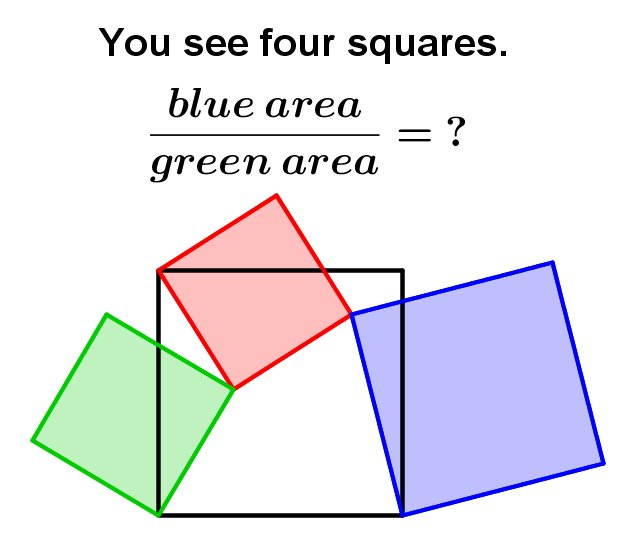
Given how it was coloured in, it seemed likely that I'd intended the question to be about the areas of the blue and green squares. The page before the puzzle was filled with variants of one of my favourite 4-squares puzzles from Henk Reuling.

I first saw this puzzle in 2018 and while I know the answer, I usually have to think a bit to convince myself of why it works; my favourite way to prove it is using similar triangles.

I still can't work out at what point I changed to one of the coloured squares having a vertex on the side of the largest square, instead of all three being hinged from the corners. I suspect the brief diversion into semicircles came after I'd moved to having two equally sized squares, but it's always possible I did it the other way round. By the bottom of the page, I've got a properly constructed version of the puzzle I ended up drawing.

2.3 Solving

The similarity to such a familiar puzzle meant that by now I was pretty sure the green square would have double the area of the blue ones. But I still needed to check – it's always embarrassing to publish something that it turns out is underspecified, and knowing what the relationship is makes it easier to choose nice numbers for the areas.

Luckily the same similar triangles explanation works, although I had to do a bit of extra work to check that the angles were actually the same. The sketches in the top-left and top-right corners of this page were enough to convince me of that.

I then went down a bit of a rabbit hole of trying to see if there was actually a nicer question hidden in here somewhere, with a long diversion into spotting 45 degree angles in various places. In the end I decided the original area question was still the nicest one, though. It was time to add some numbers (I chose 12, so that the answer would be 24, because I was publishing it on the 24th) and release it into the wilds of Twitter.

2.4 Extending

Once the puzzle had been posted, it was safe to draw around it! The angles picture from the top-right corner of the previous page kept catching my eye, so I started thinking about ways to extend that, perhaps using the similar triangles argument in a different way. This quite quickly led onto an idea for a new puzzle!

3 Solving the Puzzle (Andrew)

While Catriona's been on her break, I've had a little project of my own where I've been working through her puzzles and categorising them. My categories are in terms of how they are solved: as a teacher, I would love to make use of the puzzles in lessons but to do that then I need to know that they are accessible to the students. So I need to know what techniques are needed to solve each one.

At time of writing, this project isn't finished yet but I'm a long way through. Long enough that I've started detecting a few themes. One of those is the Agg Invariance Principle. This applies to puzzles that have a degree of flexibility in their configuration and says that since we assume that the puzzle is well-defined then it has a solution no matter how that flexibility is resolved. Often there is a particular configuration of the puzzle where the solution is obvious, or near obvious.

So it is for this puzzle. There is a freedom as to where the two blue squares meet the outer wire frame square. Different choices for this meeting point lead to different versions of the puzzle in which the solution is somewhat obvious.

What is so much fun about this puzzle is the large number of special configurations!

3.1 Vertically Aligned

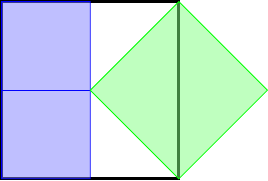
The first special configuration, shown in Figure 10, is the one I think is the most obvious. In this, the blue squares are vertical and adjacent to the left-hand edge of the outer square.

The relationship between the diagonals and sides of the blue and green squares is obvious: the diagonal of the green square is the same length as twice the side length of a blue square, or (equivalently) the side of the green square is the same length as the diagonal of a blue square. We can either use a bit of algebra to deduce that the area of the green square is twice that of a blue square, or a simple dissection to demonstrate the same.

Either way, the conclusion is that the green square has area $2\times 12=24$.

3.2 To the Right

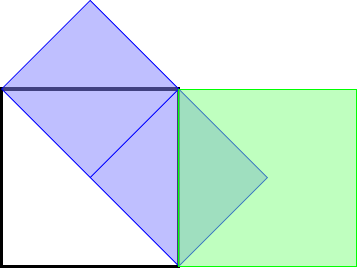
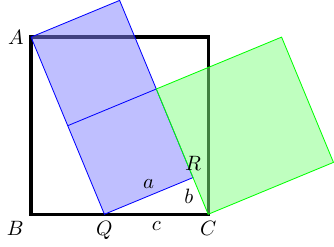
The second configuration, in Figure 11, that I saw was with the meeting point at the right-most lower vertex of the outer square, so the blue squares lie along a diagonal of the outer square.

In this case, the most obvious relationship is that a side of the green square is a diagonal of one the blue squares.

3.3 A Step to the Left

Now, it turns out that the puzzle makes sense even if the meeting point of the lower blue square and the outer square isn't inside the square at all. It just has to be on the line extending the lower edge. We then get another special configuration by putting that meeting point way over to the left, as in Figure 12.

In this configuration, the green square exactly overlaps with the outermost square, and the left-hand vertical edge of those squares is the diagonal of the uppermost blue square.

3.4 A Nice Alignment

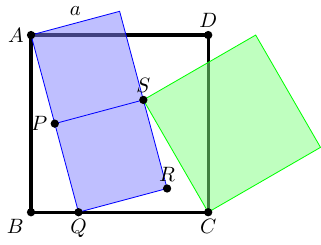
The above are probably the most obvious special configurations, but there are more. As the meeting point moves across the base of the outer square there is a point at which the edges of the blue and green squares overlap, as in Figure 13.

With the points labelled as in Figure 13, the main observation is that there are two similar right-angled triangles: $ABQ$ and $QRC$ (with the points aligning in those orders). With the sides of $QRC$ labelled as in the diagram, $AQ$ has length $2a$ so the scale factor from $QCR$ to $ABQ$ is $\frac{2a}{c}$.

The side of the outer square is therefore:

The lower edge of the outer square, $AC$, comprises $AQ$ and $QC$. The length of $QC$ is $c$ and of $BQ$ is:

As the outer square is … a square, its side lengths are the same so:

Multiplying up by $c$ gives:

There's also a relationship from applying Pythagoras' theorem to triangle $QCR$ which says that:

Putting these together:

Lastly2, we observe that $a$ is the side length of the blue square so $a^2=12$, and $a+b$ is the side length of the green square, so the green square has area $2a^2=24$.

3.5 An Isoscelean Approach

An easy deduction after solving the puzzle is that triangle $QSC$ (points labelled as in Figure 14) is isosceles. As $Q$ slides from $B$ to $C$, this starts out as a right-angled isosceles triangle and ends up as a wafer-thin triangle. So at some point in between it is equilateral. This will be when $QC$ has the same length as $QS$ and as $CS$.

We can reverse this and start with the configuration where $QC$ is one of $QS$ or $CS$ and show that in this case then it is also equal to the other one. We just have to be careful to keep in mind which one we are assuming and which we are deducing! Let's assume that $QC$ is the same length as $QS$, mainly because this is easier to figure out the drawing.

As previously, let $a$ be the side length of the blue square. Let $\alpha$ be angle $B\hat{A}Q$. Then:

By assumption, $QC$ has length $\sqrt{2}a$, so by considering the length of $BC$ and equating it to the length of $AB$ we get:

which rearranges to:

At this point, we can invoke the compound angle formula which says that:

And so ${45}^{\circ }+\alpha ={60}^{\circ }$, whence $\alpha ={15}^{\circ }$.

This is sufficient, since angle $R\hat{Q}C$ is (always) the same as angle $B\hat{A}Q$, so angle $C\hat{Q}S$ is (in this case) ${60}^{\circ }$. Then triangle $CQS$ is (by assumption) isoscelean with equal length sides $QC$ and $QS$, and with angle $C\hat{Q}S={60}^{\circ }$, hence is an equilateral triangle and so $CS$ has the same length as $QS$.

What is intriguing about this configuration is that there are several conditions we could have started with which all are necessary for triangle $QSC$ to be equilateral:

1. the equality of the lengths of $QC$ and $QS$,

2. that angle $B\hat{A}Q$ is ${15}^{\circ }$,

3. the equality of the lengths of $QC$ and $CS$,

What we have shown here is that the first implies the second, and that the first is sufficient for triangle $QSC$ to be equilateral. But we haven't quite shown that the second is sufficient, since once we had established that then we still used the first condition again to deduce that the triangle was equilateral. However, the second condition should be sufficient, since it is sufficient to draw the picture. Let us show that.

So we return to Figure 14 but now with just the assumption that angle $B\hat{A}Q$ is ${15}^{\circ }$. We still have that the lengths of $AB$ and $BQ$ are $2a\cos ({15}^{\circ })$ and $2a\sin ({15}^{\circ })$, respectively, and so the length of $QC$ is given by:

Again, we use the compound angle formula to deduce that this is the same as:

Hence $QC$ has the same length as $QS$.

The last condition, that $QC$ and $CS$ are the same length, is a little different since it puts the focus on the green square. So we have to imagine drawing the picture backwards: we start with the points $C$, $Q$, and $S$ – with $CQ$ and $CS$ the same length – and consider how to draw the rest of the diagram.

The point $R$ is constructible, since $QRS$ is a right-angled isosceles triangle with $R$ inside the triangle $QCS$. From this we can build the lower blue square and hence also the upper.

That gives us point $A$, from which we drop a perpendicular onto $QC$ to get the point $B$. However, there is no guarantee at this stage that $AB$ and $BC$ are of equal length. This is because we've just started with the assumption that $QC$ and $SC$ are the same length and this isn't always the case with the original puzzle. So we have a different set of diagrams, in which $ABCD$ is a rectangle.

For this to be a configuration of the puzzle, we therefore need to assume that $AB$ and $BC$ have the same length. This gives us the hint on how to solve it in this configuration.

Key to this solution is the observation that since triangle $QCS$ is isosceles, the points $P$, $R$, and $C$ are colinear. This means that angle $Q\hat{R}C$ is ${135}^{\circ }$.

As before, let us write $\alpha$ for angle $B\hat{A}Q$. Then $\alpha$ is also angle $C\hat{Q}R$. Since angle $Q\hat{R}C$ is ${135}^{\circ }$, this shows that angle $R\hat{C}Q={45}^{\circ }-\alpha$.

As before, let $a$ be the side length of the blue squares. Then applying the sine rule to triangle $QRC$ shows that the length of $QC$ is:

Ordinary trigonometry applied to triangle $ABQ$ shows that $AB$ and $BQ$ have respective lengths:

Then since $BC$ and $AB$ have the same length:

which simplifies to:

This time we'll use the compound angle formula for sine to deduce that:

Hence:

which gives ${45}^{\circ }-\alpha ={30}^{\circ }$ or ${150}^{\circ }$, whence $\alpha ={15}^{\circ }$ or $\alpha =-{135}^{\circ }$.

The negative angle is intriguing, but $\alpha ={15}^{\circ }$ is the solution we're looking for.

In all of these variants of the isosceles configuration then I've gone in quite heavy on the trigonometry. Normally, with Catriona's puzzles, then when I look for a special configurations then I'm hoping to make the solution "obvious3". So these aren't – to me – special configurations in that fashion but they still are special cases of the configurations.

I suspect I could remove the trigonometry (since trigonometry is just secret code for "similar triangles"), but it still feels like a bit of work is needed to solve the puzzle in these configurations.

I could very well be wrong about that!

3.6 To Infinity … Almost

The underlying assumption of these special configurations is that the problem has a unique solution, and that therefore it is independent of the exact location of the point $Q$ on the line through $BC$. I say "through" because in one of the configurations I pushed $Q$ outside the square.

We can therefore consider a little thought experiment: what happens to the diagram as $Q$ moves ever further away along the line through $BC$?

In my diagrams I've held the size of the black square constant, so effectively I've rescaled the diagram each time since actually it is the coloured squares that are fixed in size. Let's take that seriously: the black square is fixed in size and the coloured squares vary. This does mean that the question is not "What is the area of the green square?" but "What is the relationship between the blue and green regions?".

But as $Q$ moves further away from the centre then to keep the diagram on the page I do still need to do some rescaling. However, I'm now thinking of it as rescaling my point of view and not rescaling the diagram. In effect, I have to keep stepping back from the page so that I can see it all in one go. As I do that, the black square gets smaller and smaller.

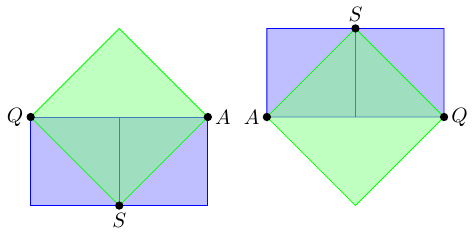
What is more interesting is what happens to the blue and green squares. As $Q$ moves further and further out, the blue squares become more and more horizontally aligned until there will come a point where the diagram is so big that I can't tell the difference any more.

At this juncture, the location of the green square depends on whether $Q$ has gone to the left or to the right. Figure 15 contains both.

In these then the original "outer" square is now so tiny that it is indistinguishable from a dot. If you zoom in a loooong way at point $A$ then you might just see it4. The corner of the green square that appears to be at $A$ is actually at the opposite corner of the "outer" square (which in other diagrams is labelled $C$) and so the corner that appears to be at $Q$ is also not quite there.

But the difference is negligible and so we can see that as $Q$ moves further away then, the ratio of the areas of the green and blue regions converges to $1$. Then we invoke the Agg Invariance Principle to say that this ratio is constant and hence must have been $1$ all along.

4 Conclusion (Andrew)

As much as I like using the Agg Invariance Principle to solve Catriona's puzzles, I do feel that it is important to sound a note of caution about it. Underneath, it relies on a measure of trust in the puzzle setter. You have to trust that the puzzle setter has done their job properly and devised a puzzle which is well-defined and only has one answer.

I'm pretty confident in Catriona for this. Not only do I have the experience of doing her puzzles, but also I've had the pleasure of discussing some of the puzzles with her and we've documented that here. Seeing pictures of her notebook and the detail that she goes into when devising a puzzle also helps.

However, I have less trust in the universe.

What I mean by this is that if a problem comes from "the real world" then I don't have the same level of trust that it is well-defined nor that it only has one answer. Indeed, there have been cases in history where the assumption that it all just works how it ought to has lead to spectacular failure.

So one can't just apply the Agg Invariance Principle to any-old mathematical problem and assume it's going to work. It is, though, sometimes the case that one can demonstrate that invariance holds without solving it and then go on to exploit that invariance to find a nice solution. The trick I use above with limits can be used in a similar fashion elsewhere.

There is a (possibly apocryphal) tale involving Napoleon, Laplace, and Lagrange wherein Laplace presented a body of work on the solar system to Napoleon who remarked that Laplace had not mentioned its creator. Laplace is said to have replied "I have no need of that hypothesis". This was later recounted to Lagrange who opined that it was a fine hypothesis in that it explained many things.

So while we might wish, with Lagrange, that we lived in a world where all our mathematical problems were set by Catriona, we should rather align ourselves with Laplace and not allow that hypothesis to prevent us digging deeper into mathematics – as, I'm sure, Catriona would wish us to be inspired by her puzzles to do.

5 Added in Proof (Andrew)

When I sent the first draft of this to Catriona, she remarked that since I was focussing on the Agg Invariance Principle then maybe she ought to put in the details of her solution by similar triangles. A few days later, I got an email from her saying that it might take a few days (sadly, "puzzle setter" is not her day job):

Having actually tried to write down my similar triangles method, it turns out it's not as simple as I thought (probably why no one did it that way!) …

Nevertheless, I agree that as I've invoked the Agg Invariance Principle in the solution section, there should be a solution somewhere that doesn't use it. When I first saw the puzzle then I did see a couple of routes that involved adding circles to the diagram, but inspired by Catriona's remark about similar triangles then I wanted to find something more direct.

I did find a really nice solution using Pythagoras' theorem, which led to some ideas that I intend to explore elsewhere, but in the end I found a very direct result which just uses simple ideas of congruency.

The key, as shown in Figure 16, is that the distance of point $S$ to the line $AB$ is the same as its distance to $BC$. One way to see this is to rotate the diagram about $S$, which has the effect of putting the upper blue square where the lower one originally was (relative to $S$). This puts the rotated $A$ where $Q$ originally was, so the rotated line segment $AB$ lies along $BC$.

This puts $S$ on the diagonal of the outer square, and so line segments $AS$ and $SC$ have the same length. This, as we've seen earlier, is enough to establish the area of the green square as twice that of the blue.

This certainly seems simpler than at least some of the versions using the Agg Invariance Principle5 so hopefully warrants its being (an) added in proof …