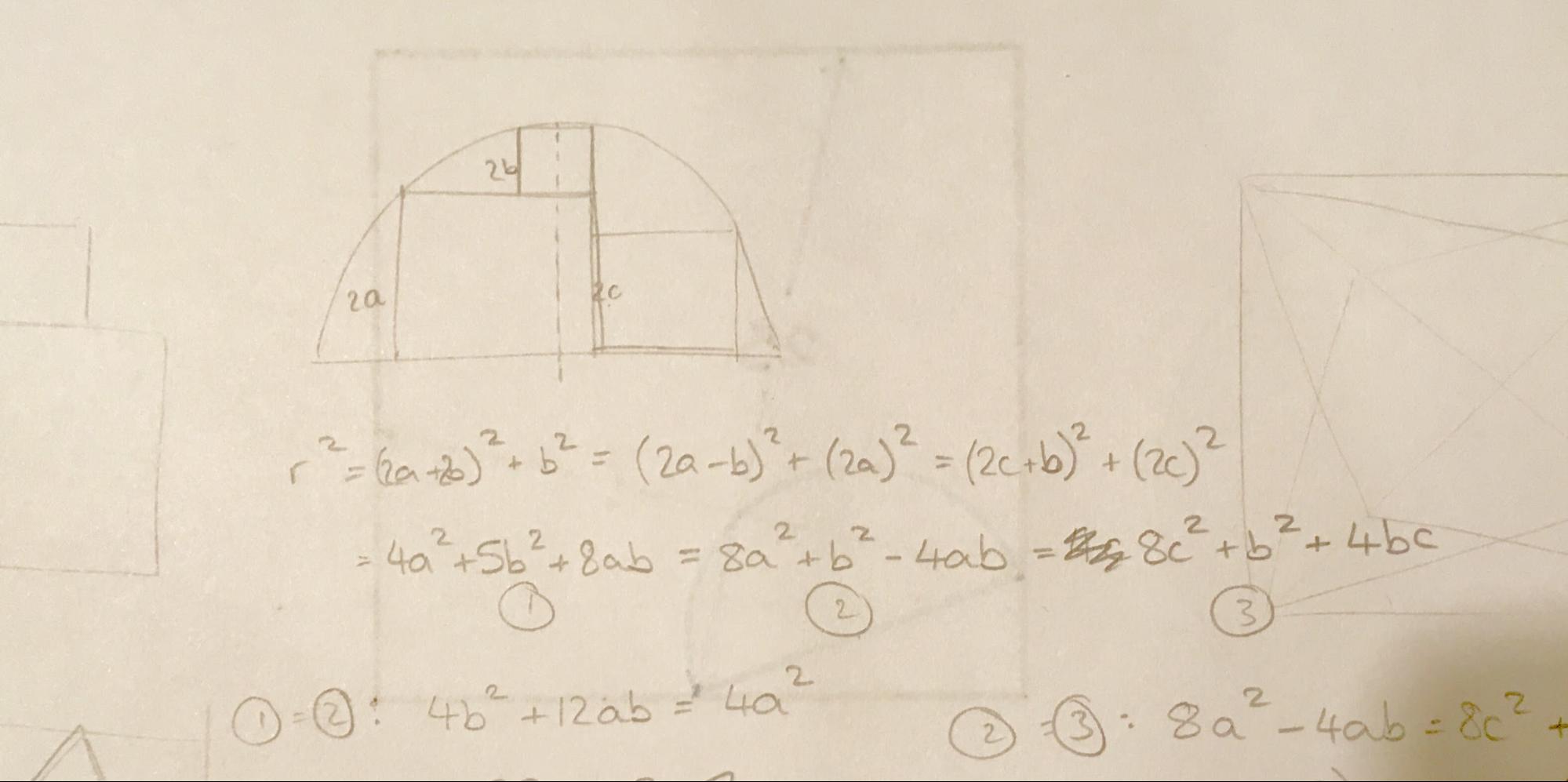1 Introduction

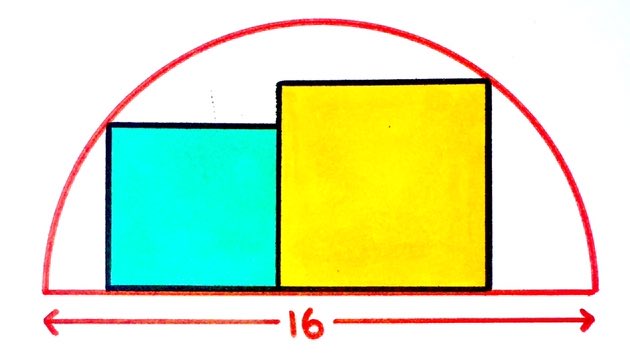
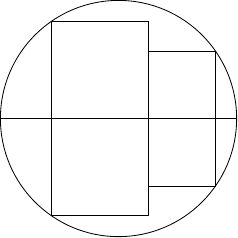
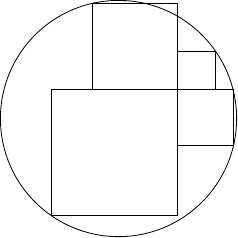
Another day, another puzzle from Catriona Shearer that sparks a whole series of spin-offs and discussions. The puzzle this time involved the areas of two squares sitting inside a semi-circle, reproduced in Figure 1.

As one commentator put it, the problem is easy to solve if you assume that it is well-defined (so that the configuration of the squares doesn't matter to the answer), but showing that it is well-defined is the difficult part.

This puzzle took on a bit of a life of its own with contributions from, amongst others, the SF author (and mathophile) Greg Egan.

The other puzzles that we've looked at have proved interesting because of the more general geometry that they've linked to. This puzzle is more self-contained: it sparks intriguing variations all by itself.

2 The Creator's Perspective, by Catriona Shearer

2.1 Creating the Puzzle

My usual approach to making a puzzle is to draw lots of pictures and scribble some algebra in the margins until I spot something that seems interesting. As a result, my notebook is usually a complete mess, with diagrams and working squeezed into any available space, around and on top of previous puzzles. The picture in Figure 2 is one of the neater pages.

One advantage of this slightly chaotic process, though, is that I end up looking back at diagrams that can often look quite different from the puzzles they developed into – if they developed into anything at all, that is. This "squares in a semicircle" puzzle is a good example of one which came from the same starting point as a previous puzzle, and is much nicer – I think – than the first.

Squares in a semicircle mark 1 was this puzzle. It had actually come about from the diagram in Figure 3, but at some point I'd decided just to focus on the two squares on top of each other, probably because all the equations I'd written down involved $a$ and $b$ but only one involved $c$.

Looking at this diagram again later, I wondered about the third square. I like puzzles that have two squares next to each other, because I'm always hoping there'll be a nice difference of two squares structure to play with, like this one here.

Even so, it came as a bit of a shock when the algebra all fell into place and I realised the total area of the two squares next to each other would be constant. I'm always very suspicious of a nice result that I had no idea about before, especially when it seems so simple. Surely I've either made a mistake, or everyone else already knows this and won't find it at all interesting. If anyone did think that about this puzzle, though, they were kind enough not to point it out – and I got the impression it was as new to others as it was to me. It really is a nice result.

2.2 Extending the puzzle

1 Completing the Square

There were lots of very clever solutions to this puzzle, but I particularly liked the ones that mirrored the semicircle (and squares) down below, in order to apply some circle theorems, such as this solution.

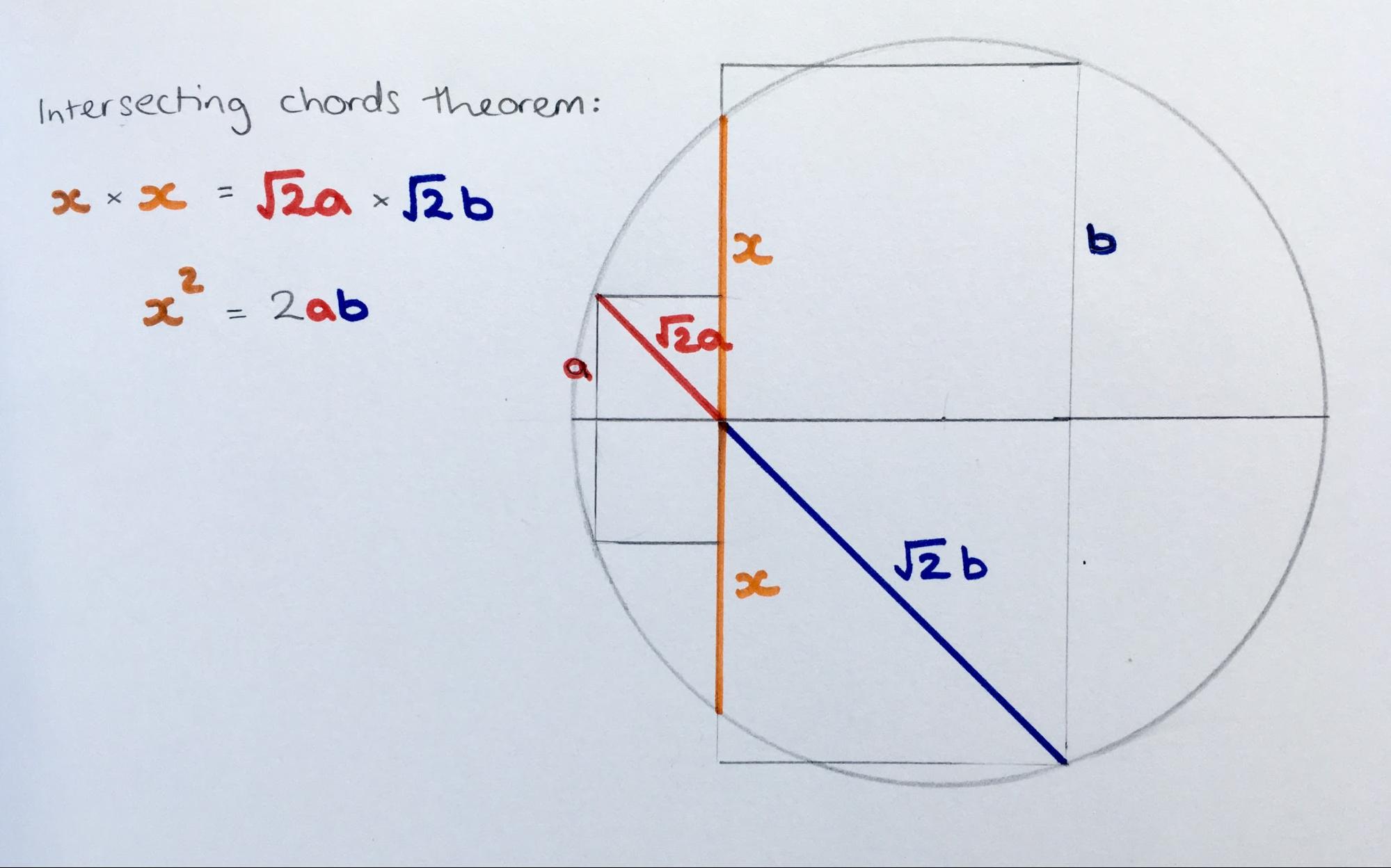
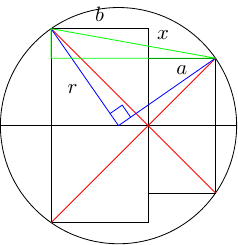
My favourite circle theorem (yes, of course I have one) is the intersecting chords theorem, which can be applied quite nicely to this diagram. It tells us that the product of the diagonals of the two squares will be equal to the square of the vertical height of the semicircle where the two squares meet, as in Figure 4.

If I draw a square which has this height, then its area is $2ab$. So the sum of areas of all three squares is $a^2+b^2+2ab=(a+b{)}^2$. This is too nice a result not to get its own puzzle!

2 Arbelos and Beyond

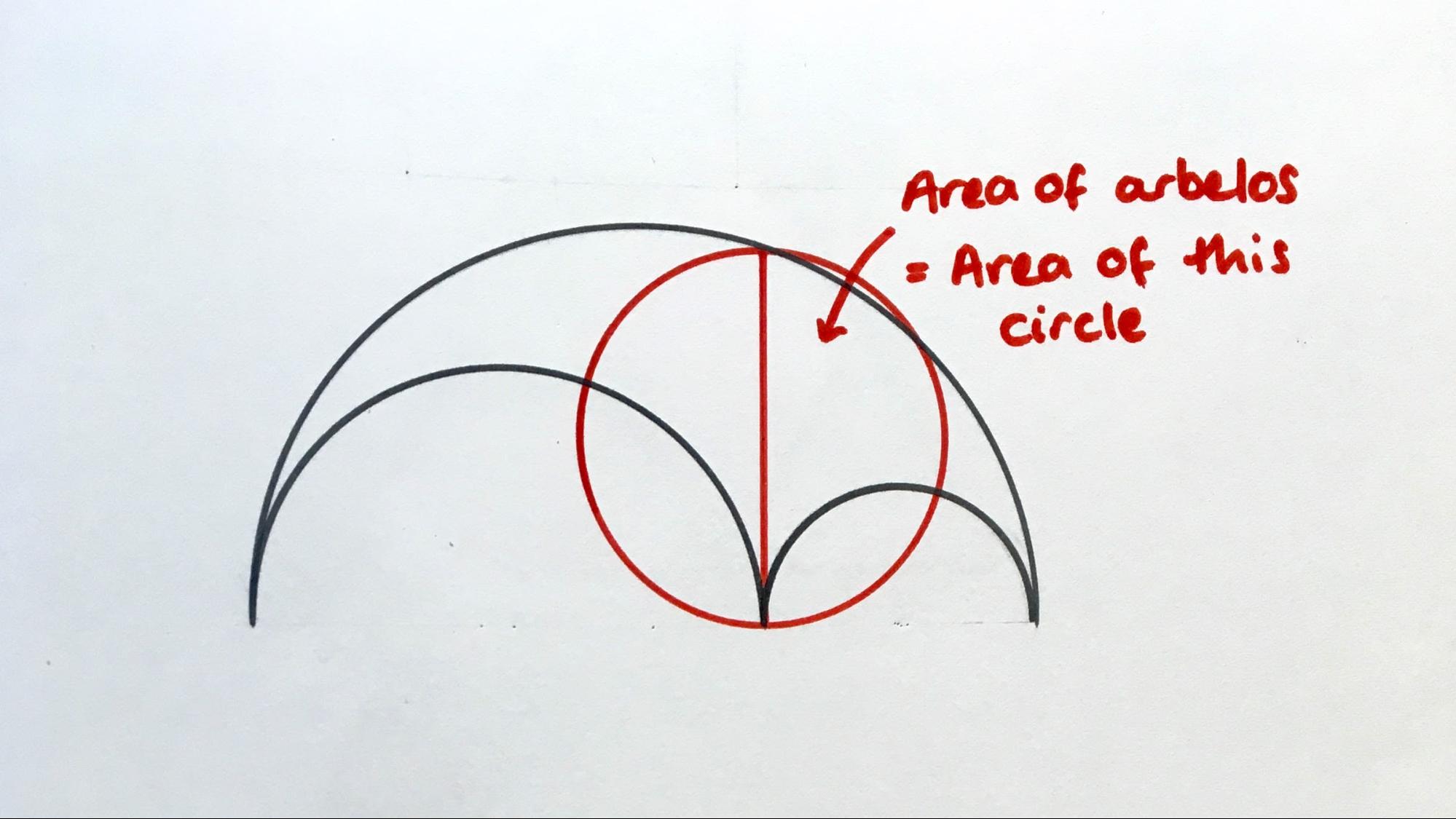
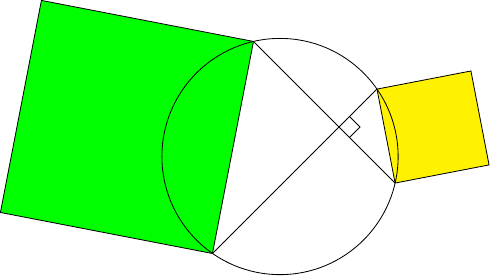
My current favourite shape (yes, I have one of those too) is the arbelos, as in Figure 5. It's constructed from three semicircles, and has a whole host of puzzle-worthy properties. I found out about the arbelos when I unwittingly drew one for a puzzle which uses one of the simpler properties: that the area of an arbelos depends only on the vertical height at the point where the two smaller semicircles meet. That puzzle was this one.

In fact, the area is equal to that of a circle which has the red line as its diameter.

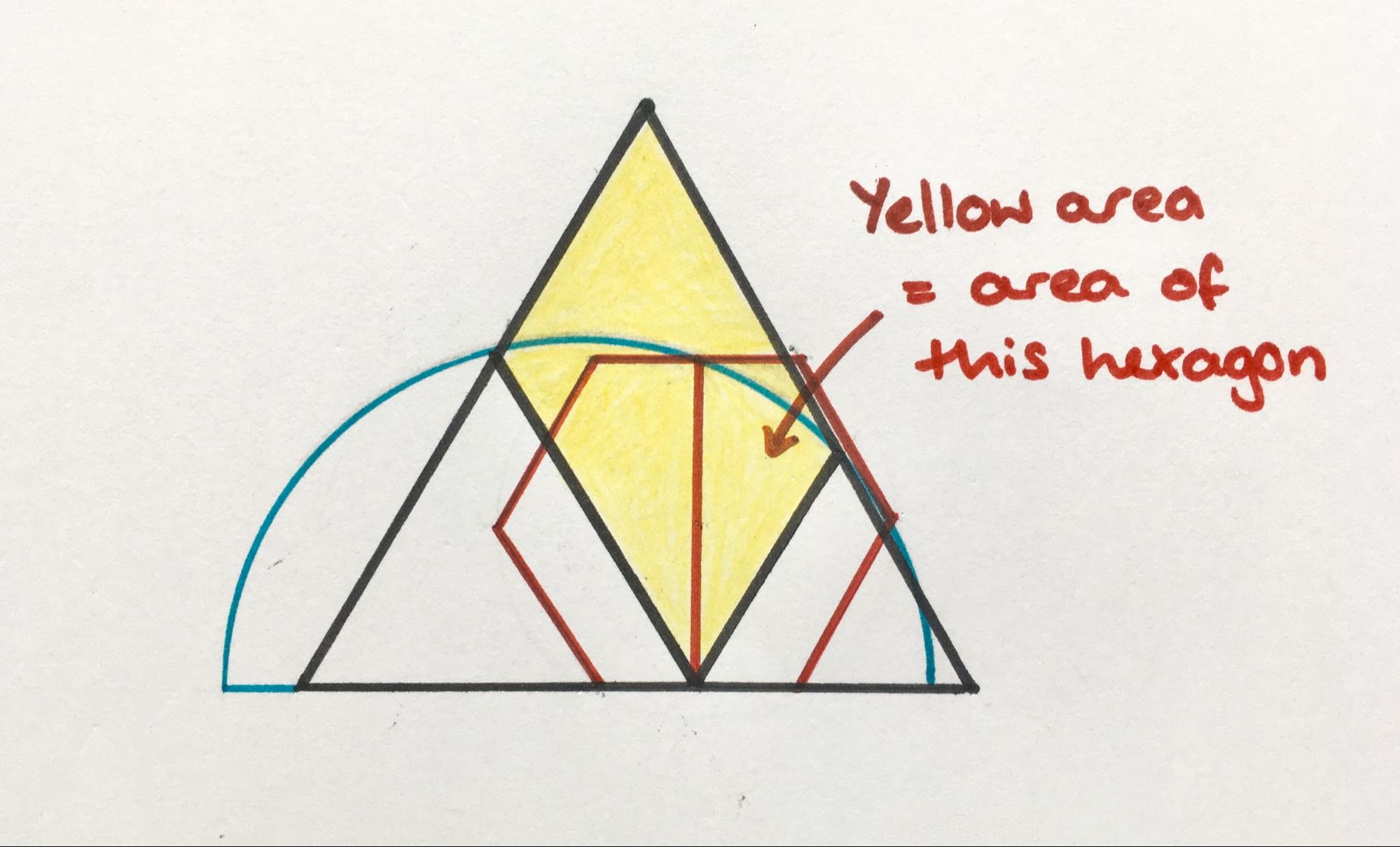
When I made the puzzle in part 1, my first thought was that this was like a squares version of the arbelos. The red square's area is equal to the "extra region" created by removing the two smaller squares from the yellow one, in the same way that the circle's area is equal to the area of the arbelos. There are a couple of differences: the semicircle is now an additional curve rather than the boundary of this extra region, and all four shapes are squares, as opposed to three semicircles and one circle. It was similar enough, though, to get me thinking about other shapes. Is there a triangle equivalent to the arbelos, for instance?

Luckily a few hours in the hall with a motivational speaker on our back to school INSET day provided some time for productive doodling. And it turns out, you can make a similar looking diagram with equilateral triangles, but the extra shape you need to add is a regular hexagon.

I haven't proved this here, but if you want to show it then a good starting place is to mirror the image down below and use the intersecting chords theorem to find the length of the red line. You'll also need to know how to find the area of equilateral triangles and hexagons.

3 The Onlooker's Perspective, by loopspace

Usually when I write about one of Catriona's puzzles it is because I've worked through a the solution which has connected with an interesting piece of geometry. For this one, although I did work through a solution, I want to write about what others did more than what I did. So the journey is a little different.

3.1 Completing the Diagram

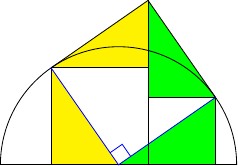
The first direction that I want to document involves adding to the diagram. It starts by adding two more squares by reflecting the original diagram in the diagonal, as in Figure 7.

I saw this first in a solution to the puzzle by Twitter user Nèstor Abad (mentioned by Catriona above). I (almost) always have a go at the puzzle myself before looking at others' solutions, and after seeing this one then I quietly threw my solution away. Figure 8 is the diagram for this.

In this figure there are two right-angled triangles involving $x$: the green triangle and the blue one. These give us:

$$\begin{array}{rl}{x}^2& =(b+a{)}^2+(b-a{)}^2=2b^2+2a^2\\ & =r^2+r^2=2r^2\end{array}$$

Hence $a^2+b^2=r^2$, and this is independent of $a$ and $b$.

Along similar lines, Vincent Pantaloni made an animation showing how to dissect the two squares to make a single square, the core idea being Figure 9.

The next step was taken by Philip Gibbs who generalised it by noting that in the diagram with four squares, viz. Figure 7, the point where the four squares met could be anywhere in the circle, as in Figure 10. In this diagram, the sum of the areas of the four squares is constant (and equal to $4$ times the square of the radius of the circle).

Finally in this direction, Vincent Pantaloni noted that the areas of the squares were in fixed proportion to the squares of the lengths of the diagonals, and these could be paired into the sides of right-angled triangles. Thus in Figure 11, the sum of the areas of the green and yellow squares is constant, regardless of where the central point lies.

3.2 Generalising the Number of Sides

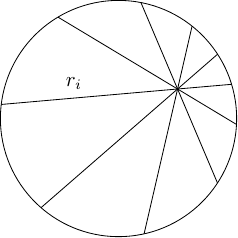
Another interesting direction on this puzzle took Philip Gibbs' version and generalised the number of lines. Greg Egan posted such a generalisation as illustrated in Figure 12. Pick a point inside the circle. Draw a number of lines, say $n$, through this point at equal angles and mark where they cross the circle (there will be $2n$ such points). Take the squares of the distances from each of these points to the original point and add them up. This is $2n$ times the square of the radius of the circle.

Greg gave a proof of this which involved working out the distances $r_i$. This used some trigonometry and solving quadratics, before noting that lots of things cancelled to make the sum simplify. Finally, OHSMaths gave a slightly simpler argument which avoided the trigonometry and quadratics.

3.3 Final Remarks

I found the evolving story of this puzzle fascinating. One thing that helped was having a go at solving each stage (or almost each stage) as that kept me aware of not just the result but also how the ideas connected. Beyond that, there were various aspects of this evolution that I'd like to highlight.

If we take Greg Egan's version to be the most general, I find it interesting that we have lost the right-angles and so there are no obvious actual squares any more. The algebraic squares appear solely due to the formula for distance in Euclidean space. Anyone familiar with my obsession with Pythagoras will not be surprised by me noticing this.

In my description of Greg's construction, I wrote about taking $n$ equiangular lines through the point giving $2n$ points on the circle. Greg described it slightly differently as taking $2n$ points on the circle satisfying an equivalent angular condition. When first investigating this construction I made a Geogebra version of it. I allowed an odd number of points around the circle. The invariance didn't hold with $3$ points, but at first it looked as though it did with $5$, $7$, or more. It was only when I increased the precision of the calculation that I saw that it didn't actually work for an odd number of points. The error was very, very small. This makes me wary of proofs or demonstrations that "show" a result without justifying it.

As a conclusion, I want to offer a rephrasing of Greg's result. A cyclic polygon is one whose vertices lie on a circle. That is to say, there is a point such that the vertices are all equi-distant from that point. Let us call that point the radial centre of the polygon.

Now consider the situation where a polygon has a point such that the vertices are all equi-angular from that point. Let us call that point the angular centre of the polygon. Note that most polygons won't have an angular centre, just as most polygons won't have a radial centre.

Greg Egan's result can be rewritten as follows.