So an online friend of mine saw a tweet about a secret society of scholars who plan to create a universe where everything is square.

The difference between circles and squares is something I've been thinking about of late because a world in which circles are squares is a world without Pythagoras' Theorem, and that's been on my mind a bit recently.

More precisely, if we take either the ${\ell }^1$ or ${\ell }^{\mathrm{\infty }}$ norm on ${ℝ}^2$ then the "unit circle" is actually a square.

But that's not replacing circles with squares. A circle or a square can be defined without regard to the ambient norm. So to actually replace circles with squares, we need something with some circles in it where replacing them by squares makes an actual difference.

1 Epicycles

Enter Epicycles. Every now and again I see a post on epicycles. Every now and again I get annoyed by a post on epicycles.

I'm not a historian of mathematics, but my reading of the story of epicycles goes something like this. Circles were viewed as a form of perfection, and the heavens (by which I really mean everything outside the atmosphere) were perfect, so therefore the heavenly bodies must move on circles. They clearly don't. So they must move on some complicated path that involves circles moving along circles. These are epicycles.

Along came Brahe, Copernicus, Kepler, and ultimately Newton who pointed out that actually everything moved on ellipses and so epicycles faded back into the aether. Until Fourier, that is, who showed that everything (for some definition of "everything") was actually made up of circles providing you used an infinite number of them. In other words, along came Fourier series.

Cue lots of posts on the internet showing how to take a shape and draw it by lots of cute circles rotating about each other at different speeds. These tend to irritate me a little, mainly because they gloss over some detail or other. For a while I had in mind writing about those details, but I couldn't think of an "in" other than that all the other posts I'd read irritated me and that didn't feel like a good basis for a post.

The theme of replacing circles with squares, however, does feel like a good basis for a post.

I do need to explain one thing about what irritates me about the way epicycles are presented. There seems to be some "wow" factor about drawing a picture with a lot of circles. To me, it is more impressive to draw a picture with as few circles as possible.

I did write a little program with the idea of fixing the number of circles and playing around with the various pictures one could get by varying the coefficients in the resulting Fourier series. But that was as far as I got until the idea of squares and circles reared its head.

2 From Circles to Squares

The key idea of replacing circles by squares is very simple: take a finite Fourier series and replace the circle functions (either $\sin (2k\pi t)$ and $\cos (2k\pi t)$ or $e^{2k\pi it}$ depending on whether you are enlightened or not) by their equivalent square functions.

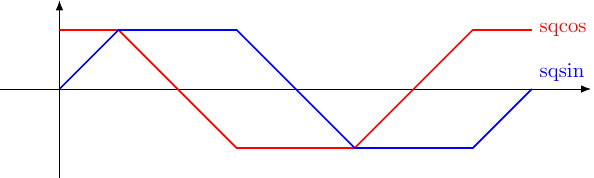
Let's unpack that a bit. We can think of the function $t\mapsto \cos (2k\pi t)$ as the function which tracks the $x$–coordinate of a point moving around the unit circle at such a speed as to go around $k$ times in $1$ unit of time. Similarly $t\mapsto \sin (2k\pi t)$ does the same for the $y$–coordinate. We want to replace these by functions that track the $x$ and $y$–coordinates of a point that moves around the unit square.

Just as for the circle, we start from $(1,0)$ and travel anticlockwise. The graphs of the coordinate functions look like Figure 1.

Their definitions look a little tricksey, but aren't all that complicated.

$$\begin{array}{rl}sqcos(t)& =\min (1,\max (-1,|8t-4|-2))\\ sqsin(t)& =sqcos(.25-t)\end{array}$$

Implementing them in code is straightforward, so I could easily add them to my little program.

My proposal, therefore, for "replacing circles with squares" is to take a finite Fourier series and replace the circle functions with their square equivalents.

It would be nice to do this for a general Fourier series, but there's a slight hitch. The square functions do not form an orthonormal basis for the appropriate space of functions. So there's no guarantee that the result of swapping the circle functions for square ones in a general Fourier series will result in a well-defined square integrable function. It may be that there is some obvious way to change the norm to make the square functions orthogonal, but I'll leave that question open for now.

3 Ticking of the Clock

The replacement idea is still not enough. I need a ready source of curves to apply this to. I quite like the idea of "a curve a day", so I started thinking about how to change a date into coefficients.

To give enough scope for variation, I considered series of the form:

$$c_{-3}{e}^{-6\pi it}+c_{-2}{e}^{-4\pi it}+c_{-1}{e}^{-2\pi it}+c_1{e}^{2\pi it}+c_2{e}^{4\pi it}+c_3{e}^{6\pi it}$$

with each $c_j\in ℂ$. I skipped $c_0$ as that would only shift the resulting shape.

So I wanted a way to convert a date into a set of values for the $c_j$. The first step is to discretise the possibilities, so rather than $c_j\in ℂ$ we consider $c_j\in \mathbb{Z}+i\mathbb{Z}$, namely complex numbers with integer real and imaginary parts (so-called Gaussian integers).

There are a few transformations that essentially preserve the resulting shape. Multiplying every coefficient by the same complex number scales and rotates the shape, while swapping $t\mapsto -t$ reflects the shape in the $x$–axis. Also, replacing $t$ by $kt$ means that we go round the shape $k$ times.

To ensure that we don't get essentially repeated shapes, we want to allow only two possibilities for $c_1$, namely $1$ or $1+i$. If we insist that $c_{-1}$ have real and imaginary components one of $-1$, $0$, or $1$ then we get $9$ choices for $c_{-1}$ for each choice of $c_1$, but some of these should be viewed as equivalent. We regard two as equivalent if they are related by a rotation, reflection, or interchanging the pair (or any combination of the two). This leaves the following choices for $c_{-1}$:

• When $c_1=1$, $c_{-1}$ can be one of $0$, $1$, $1+i$, $i$, $-1+i$, $-1$.

• When $c_1=1+i$, $c_{-1}$ can be one of $0$, $1+i$, $-1+i$, $-1-i$.

This gives $10$ choices in all.

That accounts for $c_1$ and $c_{-1}$, leaving us with four complex parameters to play with. Ideally, I'd like to say that there is a fixed set of choices and each is drawn from that set. Given a set of size $k$, we therefore have a total parameter space of $10k^4$. With $365$ days, this gives a set of size a little under $3$, which is not very big and therefore doesn't give us much freedom in generating curves. I wanted something a little more to play with.

Calendars and clocks go hand in hand, so let's try making it a time and date concept. There are $3600$ seconds in an hour and $24$ hours in a day. So the number of seconds in a year is roughly

$$3600\times 24\times 365$$

Now it just so happens that ${19}^2=361$ which is very close to both $360$ and $365$. In fact, ${19}^4=130321$ and $360\times 365=131400$, a discrepancy of a little over a thousand which is almost nothing in this context. So if we fix on a set of $19$ Gaussian integers and draw $c_{\pm 2}$ and $c_{\pm 3}$ from this set, we can use one lot to account for days and the other to account for $10$s of seconds (so the "tick" for our clock will be every $10$ seconds). It gets a bit confusing to refer to "$10$s of seconds" with all the numbers flying around, so I'm going to use the term "decasecond".

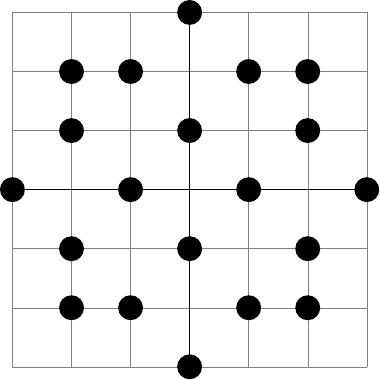
This leaves us with just the hours. We have a factor of $10$ from the choices of $c_1$ and $c_{-1}$. If we could just leverage that up to $12$ then we'd have the hours up to a.m. and p.m., with then a factor of $2$ to finish with. We have $6$ options when $c_1=1$, but only $4$ when $c_1=1+i$. So if we add in two more for when $c_1=1+i$ we'll be home and dry. Adding in $2i$ and $-2$ provides a pleasing symmetry, and while the choice of, say, $c_1=1+i$ and $c_{-1}=2i$ is related to the choice of $c_1=1$ and $c_{-1}=1+i$ by multiplication by $1+i$, if we pick our $19$ points for the other coefficients carefully we won't get any duplicated pictures.

Let's choose those $19$ points. I have to admit, $19$ is a strange number to be choosing as it affords very little symmetry. Figure 2 is what I ended up with. (Though if you count the points, you'll find that there are twenty – so for each of the four coefficients I remove one of the four innermost points.)

The final step is the factor of $2$ from the morning and afternoon split. But here's where the circles and squares comes to the rescue: one is circles, the other squares.

4 Mixing it up

The final step was to mix up the choices. The way I have laid it out above, the obvious course is to take a date and time and write it as a triple using days (of the year), hours (of the day), and decaseconds (of the hour).

At time of writing, we are at the $105$th day of the year, $17$th hour of the day, and approximately $315$th decasecond of the hour. Then we take the $105$ and the $315$ and write them in base $19$ as $5\mid 10$ and $16\mid 11$, respectively. Finally, we write the $17$ in base $12$ as $1\mid 5$. We therefore have our numbers as:

$$(5,10,1,5,16,11)$$

So we can use the $5$ and $10$ to choose $c_2$ and $c_{-2}$, the $16$ and $11$ to choose the $c_3$ and $c_{-3}$, the $5$ tells us which pair to pick for $c_1$ and $c_{-1}$, and the $1$ tells us whether to use squares or circles.

The problem with this is that it is all rather too predictable. Only one number is guaranteed to change every decasecond and all morning pictures will use circles.

So let's mix it up.

I'll show what I do with the numbers given above: $105$th day of the year, $17$th hour of the day, and $315$th decasecond of the hour.

The first thing is to use the parity (by which I mean "odd/even"ness) of the decasecond number to set the circle/square choice. Rather than swapping every decasecond, what I decided to do was to swap every odd decasecond, so the sequence goes "square", "circle", "circle", "square". This means that every decasecond we either swap between using squares and using circles, or we change our coefficients. I quite like the effect of this as it means that the change in type and change of coefficients happen at different steps.

Once we've used the parity of the decaseconds to determine whether we're using squares or circles, we need to remove it from consideration. This means that we round $315$ down to the nearest even number, in this case $314$.

Our decaseconds count now only has half the information it had before, so we augment it back up to full strength using the "morning/afternoon"ness of the hour. In this case, $17$ is afternoon so we add $1$ to the decaseconds and replace $17$ by its equivalent on a $12$ hour clock (with a slight modification that we use $0$ instead of $12$). So we're back to $315$ decaseconds but now have $5$ hours.

We'll use the $5$ hours to set $c_1$ and $c_{-1}$. We start by using its "odd/even"ness to set $c_1$: $5$ is odd so we take $c_1=1+i$. Then we divide $5$ by $2$ and throw away any remainder to get $2$. We use this number to choose one of the $6$ choices for $c_{-1}$. The formula I used was to use its "odd/even"ness to choose the imaginary component (in this case $0$), then again dividing by $2$ and throwing away the remainder gives us one of $0$, $1$, or $2$, in this case $1$. Subtracting $1$ maps this to $-1$, $0$, or $1$ which gives us the real part, in this case $0$. So our resulting number is actually $0$. Finally, we multiply that by $c_1$ to get the correct choice for $c_{-1}$.

Now we look at our two numbers for days of the year and decaseconds of the hour. We want to mix these together in a fashion that means that we still get a unique set of choices for the remaining $c_k$ (ignoring, that is, the minor issue of the discrepancy between $360\times 365$ and ${361}^2$ – we basically ignore that).

Our numbers of days and decaseconds will be changing by one each time they change (apart from on the wrap around). So we make it so that a change by one in these numbers means a bigger change in the numbers we actually use. To do that we multiply them by some fixed number, and then take remainders on dividing by $361$. To ensure that when we do that we don't lose any information, we need to pick our fixed number carefully – it needs to be invertible modulo $361$, meaning that it must not have any factors in common with $361$. We'd also like it to be quite big, somewhere in the middle of $361$, to have the biggest disruptive effect. I picked $127$.

So we multiply our numbers by $127$ and then take remainders modulo $361$. This mixes up the numbers without losing information. It doesn't, though, change the fact that one of the numbers only changes each day. My solution to that is to combine the number of decaseconds with the number of days in such a fashion that if we know the combination and the number of decaseconds then we could recover the number of days (this means that we don't lose any information). By combining this with multiplying by $127$, we can mix up these numbers quite considerably without changing the amount of information contained in them.

The procedure I went for was the following. Start by multiplying the decaseconds by $127$, in our example we get $40005$. We'll take its remainder after dividing by $361$ to get one of our numbers, which will be $295$. This throws away the quotient, which is $110$, so we'll add that to our other number, to get $215$ in our example. Now multiply that by $127$ and take its remainder on dividing by $361$, in our case we get $230$.

So from our original numbers of $315$ and $105$ we have generated two new numbers $295$ and $230$. Let's see what happens to those numbers as the seconds tick by.

$$\begin{array}{rl}315,105& \mapsto 295,230\\ 316,105& \mapsto 61,357\\ 317,105& \mapsto 188,357\\ 318,105& \mapsto 315,357\\ 319,105& \mapsto 81,123\end{array}$$

And finally, we convert each of those numbers to a pair of numbers less than $19$ to pick one of our chosen points as the coefficient.

The last step in designing the clock is to figure out what to do with the $10$ seconds between each change. As we're drawing a shape, I use $8$ of those seconds to trace round it and then the final $2$ seconds to morph from one shape to the next.

The result is the animation at the top of the page. A more intricate version (showing the construction details) can be found on my code pages with source on github.