Triangles and Identities

loopspace

2024-10-08

Contents

Home
1. Introduction
2. cot plus tan
3. Double angle formulae
4. A complicated tangent
5. Sine rule
6. Tans and Cots
7. Average Tangent
8. Double Angle Tangent
9. One diagram, many identities

1 Introduction

Of late, I've become a bit obsessed with similar triangles. My contention is that that vast majority of school geometry is built upon the properties of similar triangles. In particular, all trigonometry is about similar triangles1.

1The name "trigonometry", roughly translating to "measuring triangles", slightly gives it away.

This obsession has found a new outlet as I've marked a lot of trigonometry questions recently. My new hobby is that whenever I see a trig identity I try to find a picture that demonstrates it. At the level of questions I'm encountering, most of the trig identities depend on a series of substitutions involving Pythagoras, the compound angle formulae, or the relationships between the different ratios. All of these can be shown by suitable diagrams, so anything that depends on them ought to be demonstrable by a suitable diagram.

My goal with each diagram is that it illustrate the given identity as written.

I'm recording the pictures that I figure out here for "posterity". I'll add more as I encounter them. I'll also be happy to consider any challenges I'm sent.

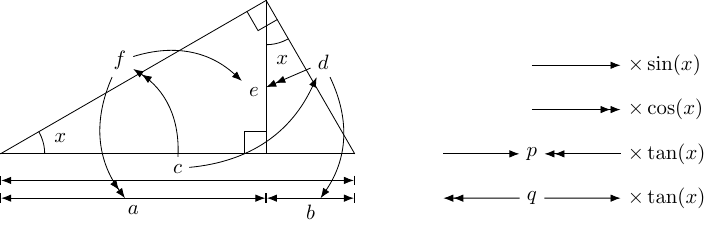
2 cot plus tan

\cot (x) + \tan (x) = 2 cosec (2 x)

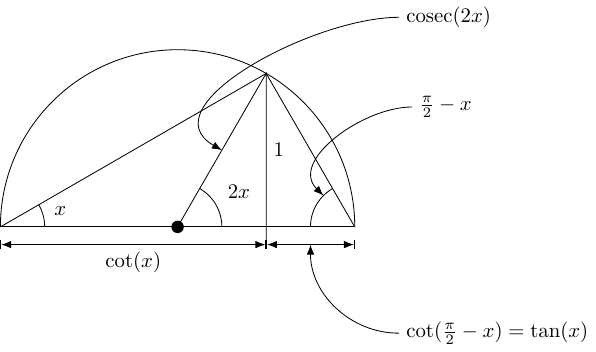
3 Double angle formulae

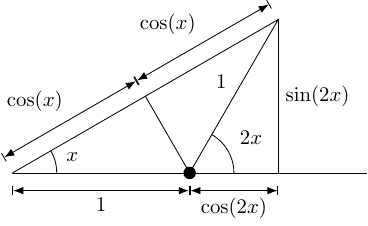
\begin{aligned} 2 \cos (x) \sin (x) & = \sin (2 x) \\ 2 \cos (x) \cos (x) & = 1 + \cos (2 x) \\ \tan (x) & = \frac{\sin (2 x)}{1 + \cos (2 x)} \end{aligned}

4 A complicated tangent

\frac{\sin (x) + \sin (2 x)}{\cos (x) + 1 + \cos (2 x)} = \tan (x)

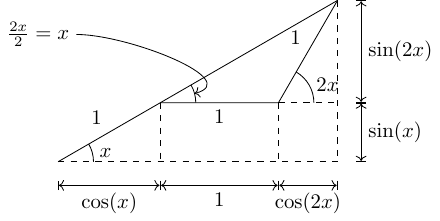
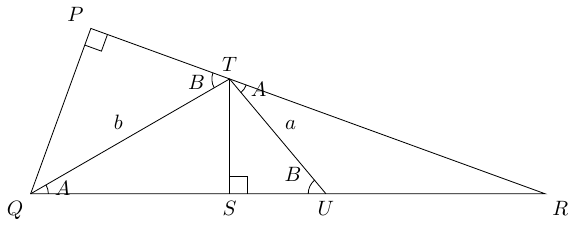
5 Sine rule

\frac{b}{a} = \frac{\sin (B)}{\sin (A)}

\begin{aligned} T S & = b \sin (A) \\ P Q & = b \sin (B) \\ Δ P Q R & ≃ Δ S T R \\ \Rightarrow \frac{\sin (B)}{\sin (A)} & = \frac{b}{a} \end{aligned}

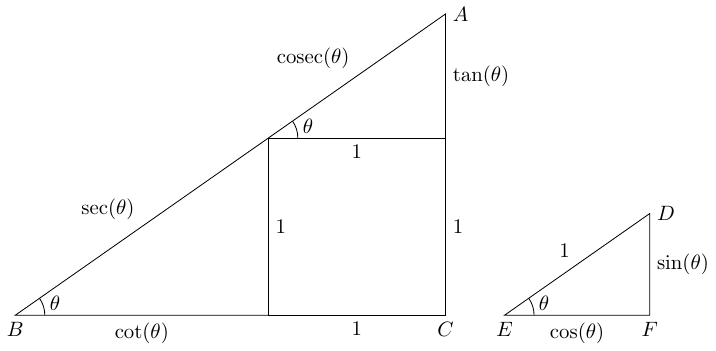
6 Tans and Cots

\frac{\tan (θ) + 1}{\sin (θ)} = \frac{\cot (θ) + 1}{\cos (θ)}

Δ A B C ≃ Δ D E F \Rightarrow \frac{\cot (θ) + 1}{\cos (θ)} = \frac{\tan (θ) + 1}{\sin (θ)} = \sec (θ) + cosec (θ)

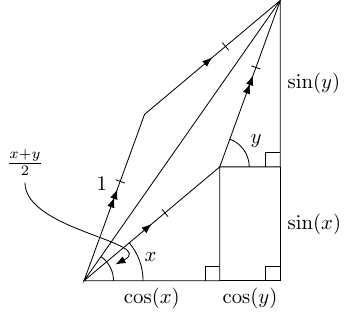
7 Average Tangent

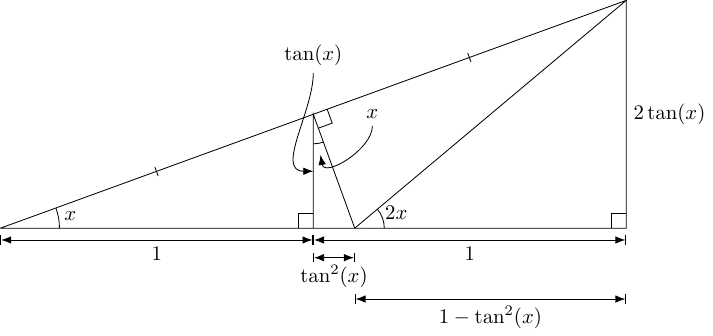
\tan (\frac{x + y}{2}) = \frac{\sin (x) + \sin (y)}{\cos (x) + \cos (y)}

8 Double Angle Tangent

In the Double Angle section above, I didn't include the standard formula for the tangent of the double angle.

\tan (2 x) = \frac{2 \tan (x)}{1 - \tan^{2} (x)}

9 One diagram, many identities

\begin{aligned} a + b & = c \\ a & = 1 : & 1 + \tan^{2} (x) & = \sec^{2} (x) \\ b & = 1 : & \cot^{2} (x) + 1 & = {cosec}^{2} (x) \\ c & = 1 : & \cos^{2} (x) + \sin^{2} (x) & = 1 \\ d & = 1 : & \cot (x) \cos (x) + \sin (x) & = cosec (x) \\ e & = 1 : & \cot (x) + \tan (x) & = cosec (x) \sec (x) \\ f & = 1 : & \cos (x) + \sin (x) \tan (x) & = \sec (x) \end{aligned}