1 Introduction

The basic problem in graphical programming is that of taking a three dimensional object and rendering it onto a two dimemsional screen. Stated this way, it is a question of how to project ${ℝ}^3$ onto ${ℝ}^2$. However, there is another layer in that it may be easiest to define the object in a different set of coordinates to the "world" coordinates.

So we have three sets of coordinates. The model's coordinates, the world's coordinates, and the screen coordinates. And transformations between these.

2 A Model

Let's take a simple example. A cube. Imagine we want to put a cube somewhere in space. It isn't hard to define a cube of a particular size and at a particular point, but a rotated cube can be a bit tricky so it is much easier to define a cube at the origin and in the standard orienation and then move it to where it is wanted.

-- set up a mesh for the cube
cube = mesh()
-- we first define a table containing the corners and colours at
-- those corners from which we'll sample when building our mesh
local corners = {}
for l=0,7 do
    i,j,k=l%2,math.floor(l/2)%2,math.floor(l/4)%2
    table.insert(corners,{vec3(i,j,k),color(255*i,255*j,255*k)})
end
-- These two tables will be passed to the mesh in a moment
local vertices = {}
local colours = {}
local u
-- We now iterate as follows:
-- We group the faces of the cube into three pairs of opposite faces
-- the 'l' variable iterates through these pairs
-- the 'i' variable selects a face of that pair
-- each face has two triangles, 'k' selects the triangle
-- each triangle has three vertices, 'j' selects the vertex
for l=0,2 do
    for i=0,1 do
        for k=0,1 do
            for j=0,2 do
                u = (i*2^l + ((j+k)%2)*2^((l+1)%3)
                    + (math.floor((j+k)/2)%2)*2^((l+2)%3)) + 1
                table.insert(vertices,corners[u][1])
                table.insert(colours,corners[u][2])
            end
        end
    end
end
-- Now we pass these to the mesh
cube.vertices = vertices
cube.colors = colours

3 Seeing the Cube

If we just cube:draw() then we won't see much. That's because a cube of side length 1 is not very big on the screen. To see it properly we need to shift our viewpoint. For now, we can think of this as a bit of magic that puts us in the right spot to see our cube.

function draw()
    background(40, 40, 50)
    perspective(40, WIDTH/HEIGHT)

    camera(10,10,10,  0,0,0,  0,1,0)
    cube:draw()
end

4 Moving the Cube

So now let's move the cube. Actually, we'll duplicate it and move it so that we can be sure that it has moved. A single operation is fairly straightforward. If we didn't want to delve into matrices, we'd have a choice of three operations: rotate, scale, and translate. We can see the effect of each of these by changing our draw() function a little.

function draw()
    background(40, 40, 50)
    perspective(40, WIDTH/HEIGHT)

    camera(10,10,10,  0,0,0,  0,1,0)
    cube:draw()
    translate(2,3,4)
    cube:draw()
    resetMatrix()
    rotate(90,0,1,0)
    cube:draw()
    resetMatrix()
    scale(1,-2,.5)
    cube:draw()
end

The resetMatrix() calls ensure that we only apply one transformation each time.

5 Composition

Now comes the complicated bit. What happens if we want to do two things? The essential thing to remember here is that the order of doing things matters. There is a Norwegian children's song the start of which roughly translates as "Open window, lean out". Do that the other way around and you're in trouble.

So order matters. But that isn't all. The problem with composition is that it happens the wrong way around. When we write an expression like $\sin (\cos (x))$ then this means "take $x$, apply $\cos$, then apply $\sin$." We work from the inside to the outside and that usually means working in reverse order. (For a complicated example, consider $3x+4$. Then try $4+3x$. Now have a lie down.)

The same happens in Codea. When you write something like the following,

translate(1,2,3)
rotate(45,1,1,1)
cube:draw()

Then you are setting up the transformation to be applied and it is working according to the above rules. So you should think of a great big parenthesis after each statement. Read it as follows.

translate(1,2,3)(
  rotate(45,1,1,1)(
    cube:draw()
  )
)

And each transformation means "apply this transformation to whatever is inside".

Obviously, it's good to experiment. A good experiment to do is to translate along an axis and rotate around another axis. Try this both ways around (and I recommend rotating by ${45}^{\circ }$).

6 Matrices

So what does this all have to do with matrices? Once you get beyond simple lists of transformations, you might want to be able to store and restore the current transformation. For this, it wouldn't be necessary to really know how Codea stores the transformation, you would just need a save-to-variable and restore-from-variable functionality without ever actually knowing the structure of the variable. But once you introduce the facility to save and restore the transformation, it doesn't take a large leap to realise that it might be useful to be able to manipulate it in between times. Again, one could do all of this via methods without knowing what is going on underneath, but a glimpse under the bonnet ("hood" for Americans) can make it easier to understand and thus easier to achieve the desired end.

Translations, rotations, and scalings are all examples of affine transformations. Exactly what these are isn't important – I include the name so you know what to look for if you want to learn more. What is important is how much information is needed to completely specify one of these. The answer is: not a lot. Once you know where the origin and the three standard vectors go, you know everything. The three standard vectors are the ones with a $1$ in a single place and zeros elsewhere. As we're in three dimensions, we will write these as $\stackrel{\rightharpoonup }{i}$, $\stackrel{\rightharpoonup }{j}$, and $\stackrel{\rightharpoonup }{k}$.

To recover the transformation, if, say, the origin goes to $\stackrel{\rightharpoonup }{b}$ and the others go to ${\stackrel{\rightharpoonup }{a}}_1+\stackrel{\rightharpoonup }{b}$, ${\stackrel{\rightharpoonup }{a}}_2+\stackrel{\rightharpoonup }{b}$, and ${\stackrel{\rightharpoonup }{a}}_3+\stackrel{\rightharpoonup }{b}$ then an arbitrary vector $x\stackrel{\rightharpoonup }{i}+y\stackrel{\rightharpoonup }{j}+z\stackrel{\rightharpoonup }{k}$ goes to $x{\stackrel{\rightharpoonup }{a}}_1+y{\stackrel{\rightharpoonup }{a}}_2+z{\stackrel{\rightharpoonup }{a}}_3+\stackrel{\rightharpoonup }{b}$.

So to store a transformation, we need to store four vectors of length three. In other words, a 2-dimensional array of numbers of size 4 by 3.

For reasons that are slightly to do with implementation and slightly mathematical, Codea actually stores them as a $4\times 4$ double array, aka a $4\times 4$ matrix. The vector that the origin goes to is promoted to length $4$ by adding a $1$ in the fourth place. The others have a zero. Note that the vectors that we record are ${\stackrel{\rightharpoonup }{a}}_1$ etc. which aren't quite where the three vectors $\stackrel{\rightharpoonup }{i}$ etc. go to but are rather taken relative to where the origin goes to.

Now we get to a complicated bit. Vectors are lists of numbers. Lists can be written either across or down. It's a choice and it has to be made and then stuck to. Slightly unfortunately, OpenGL (and therefore Codea) chose a different convention to most of the rest of the world. Vectors in Codea are written horizontally.

Why does this matter? If you just regard matrices as storage pots for transformations then it doesn't. But if you want to manipulate the transformation by changing its matrix then it matters because it tells you how and what to change.

Let's start with a simple example. Suppose we have two matrices $A$ and $B$ which we've generated by some processes. These represent two transformations. We want to apply them both so that the transformation represented by $A$ is done before that represented by $B$. Remember that if we were writing the commands directly in our program then this would mean that we would write the commands for $B$ first. This combined transformation is also represented by a matrix. Let's call it $C$. Clearly there is some way to figure out what $C$ is from knowing $A$ and $B$ as those completely describe it. The method for doing this is called matrix multiplication. It behaves a lot like multiplication of numbers but with one crucial difference. Remember what I said about order being important? That carries over to matrices as well: the order of multiplication matters.

So which is it? Is it that $C=AB$ or $C=BA$? Here's where the convention on how to write vectors comes in. Because we are writing them across, when a matrix, say $M$, transforms a vector, say $v$, then we have to write that as $vM$. That is to say, $vM$ is a new vector and is the result of applying the transformation represented by $M$ to the vector $v$. Now if we want to do $A$ before $B$ then clearly we need to put $A$ nearest the vector. So $vC=vAB$, whence $C=AB$.

The slightly crazy thing about this is that to write out the corresponding commands explicitly we would list those for $B$ before those for $A$. But in both cases, it is the one nearest the vector that gets applied first.

You can test this using the following code.

rotate(90,0,1,0)
mb = modelMatrix()
resetMatrix()
rotate(90,1,0,0)
ma = modelMatrix()
resetMatrix()
rotate(90,0,1,0)
rotate(90,1,0,0)
mc = modelMatrix()
print(mc)
print(ma*mb)
print(mb*ma)

7 Manipulating Matrices

We can read off the current model matrix by m = modelMatrix() and restore it by modelMatrix(m). If we want to manipulate m in the meantime then we can use some useful methods. Writing m = m:rotate(45,1,0,0) means that we change m by the right amount so that we put in place another rotation. This is fine if you can figure out how to write your transformation as a combination of translations, rotations, and scalings. But sometimes it is easier just to work it out directly. After all, what you need to know is where four points end up and sometimes that's really easy to see.

If you do know where the origin and the four elementary vectors go then writing down the matrix is easy. You just have to remember that everything is written across. Then list the vectors according to the list: first, where $\stackrel{\rightharpoonup }{i}$, then $\stackrel{\rightharpoonup }{j}$, then $\stackrel{\rightharpoonup }{k}$ go (relative to where the origin goes), lastly where the origin goes. You also have to promote them to length $4$ by making the last column look like $0,0,0,1$.

$$\left[\begin{array}{cccc}1& 2& 3& 0\\ 4& 5& 6& 0\\ 7& 8& 9& 0\\ 10& 11& 12& 1\end{array}\right]$$

So much for setting the matrix. What about working out what a matrix does to a particular vector? The transformations are done by the GPU and the results are not made available to Codea so if you need to know where a particular vector will end up then you need to do the maths yourself. Unfortunately, although Codea has a vec4 object, it doesn't yet have a function to natively multiply a vector by a matrix. Whilst it would be possible to write one, it is possible to co-opt the inbuilt functions to provide one.

This works by using the translation transformation. Suppose that $P$ is our mystery transformation and we want to know what it does to a vector $\stackrel{\rightharpoonup }{v}$. So we want to know $P(\stackrel{\rightharpoonup }{v})$. Let $T_{\stackrel{\rightharpoonup }{v}}$ represent the transformation that translates everything by $\stackrel{\rightharpoonup }{v}$. Then $T_{\stackrel{\rightharpoonup }{v}}(\stackrel{\rightharpoonup }{0})=\stackrel{\rightharpoonup }{v}$. So $P(\stackrel{\rightharpoonup }{v})=P(T_{\stackrel{\rightharpoonup }{v}}(\stackrel{\rightharpoonup }{0}))$.

In terms of the matrices in Codea, we do mv = m:translate(v.x,v.y,v.z) and then read off vec3(mv[13],mv[14],mv[15]). This is where $v$ goes under the influence of $m$.

Actually, we should divide by m[16] but so far we've behaved ourselves and not done anything strange so this will be a $1$.

8 A Little Bit Deeper

Let's drop down a dimension. Let's imagine that we're really interested in the plane, and in affine transformations thereof. Following the above description, we should be using $3\times 3$–matrices to represent these.

Now, matrices really represent linear transformations. A transformation is linear if it respects sums and scales. That is to say, it doesn't matter if you add then transform or transform then add; the answer is the same either way. One key property of such transformations is that they keep the origin fixed. This isn't true of affine transformations as these allow for translations.

So how do we get from two dimensional affine transformations to three dimensional linear ones? The answer is both neat and sneaky. Instead of thinking of the plane as the $x-y$–plane in space we shift it out one unit along the $z$–axis. So the origin on our plane is no longer at the origin in space and can therefore be moved around by linear transformations of the ambient space.

The process works, therefore, like this. We take a point $(x,y)$ in the plane. We promote that to $\stackrel{\rightharpoonup }{v}=(x,y,1)$ in $3$–space. Then apply a matrix, say $M$, to get $\stackrel{\rightharpoonup }{v}M$ still in $3$–space. What happens now is interesting. We want to end up with a point on the plane so we need to drop down a dimension. The simple case is if the vector $\stackrel{\rightharpoonup }{v}M$ is of the form $(x\text{'},y\text{'},1)$ as then we just take $(x\text{'},y\text{'})$. But this isn't necessarily the case. $M$ could have been anything so there is no reason why $M$ should have kept the $z$–value equal to $1$. What should happen if we end up with, say, $(2,3,2)$?

The boring answer is for this to lead to an error: "I'm afraid I can't do that, Dave.". It is possible to restrict to only those matrices that keep the $z$–value equal to $1$ (as we'll see in a moment, these correspond to the affine transformations of the plane). But it's more interesting, and opens up intriguing possibilities, for the system to try to do something with these coordinates.

What should it do? Again, there's a boring answer: just take the $x$ and $y$ values. What actually happens is much better and can be understood very simply. Imagine you are standing at the origin and are looking out at space. The object you are concerned with is out there, somewhere. Not necessarily on the $z=1$ plane, though. So what you do is you put a big sheet of glass in front of you in the $z=1$ plane. As it is glass, you can see your object through it. Now draw the object on the glass exactly as you see it. That's what the OpenGL system does.

This makes it possible to do more interesting transformations. An affine transformation applied to a square can change the lengths and angles a bit, but it can't stop opposite sides being the same length and angle. This extra projection step can. It introduces perspective so you can put one side further away which makes it smaller.

The formula is that $(x\text{'},y\text{'},z\text{'})$ goes to $(x\text{'}/z\text{'},y\text{'}/z\text{'})$. There's a slight problem with that. What if $z\text{'}=0$? What that means is that that point is "at infinity" meaning that you would almost certainly have to turn your head to see it and definitely could not see it through the glass. Whilst in theory we should worry about this, in practice any point at or near "infinity" will be off the screen and so not a point we should worry about (it's not quite that simple but that will do to a first approximation).

Let's conclude this section with a few formulae. Multiplying a vector by a matrix works according to the following equation.

$$\left[\begin{array}{ccc}x& y& z\end{array}\right]\left[\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right]=\left[\begin{array}{ccc}xa+yd+zg& xb+ye+zh& xc+yf+zi\end{array}\right]$$

But in our case, we start with $z=1$ and divide by the $z$–value. So the total transformation is:

$$\left[\begin{array}{cc}x& y\end{array}\right]\mapsto \left[\begin{array}{cc}\frac{xa+yb+g}{xc+yf+i}& \frac{xb+ye+h}{xc+yf+i}\end{array}\right]$$

From this we can see that if $c=f=0$ and $i\ne 0$ then there is no difficulty with the division. Moreover, in this situation then the different possibilities for $i$ are not interesting as they provide simply another scale factor. The corresponding matrices are of the form:

$$\left[\begin{array}{ccc}a& b& 0\\ d& e& 0\\ g& h& 1\end{array}\right]$$

which are precisely those corresponding to affine transformations of the plane.

If, however, $c$ and $f$ are not both zero, it will always be possible to find $x$ and $y$ to make the denominator zero. There is always a "danger line", or "vanishing line". But away from this line, we can get interesting behaviour.

Going back up to $3$–dimensional space, the overall transformation is the following. We start with $(x,y,z)$ and then apply the matrix to the augmented vector $(x,y,z,1)$. This results in a vector of the form $(x\text{'},y\text{'},z\text{'},w\text{'})$. At this point, anything with an $x\text{'}$ or $y\text{'}$ or $z\text{'}$ bigger than its $w\text{'}$ is thrown away. These points won't be on the screen so there is no point in processing them further. Next, the first three coordinates are divided by $w\text{'}$. This is where the fancy perspective stuff takes place, if at all. Lastly, the $x"$ and $y"$ coordinates (which now have values in $[-1,1]$) are mapped to ths screen. The remaining $z"$ coordinate is used to work out what is behind what (and so what is not drawn).

$$\begin{array}{rl}\left[\begin{array}{ccc}x& y& z\end{array}\right]& \mapsto \left[\begin{array}{cccc}x\text{'}& y\text{'}& z\text{'}& w\text{'}\end{array}\right]=\left[\begin{array}{cccc}x& y& z& 1\end{array}\right]M\\ & \mapsto \left[\begin{array}{ccc}x"& y"& z"\end{array}\right]=\left[\begin{array}{ccc}x\text{'}/w\text{'}& y\text{'}/w\text{'}& z\text{'}/w\text{'}\end{array}\right]\\ & \mapsto \left[\begin{array}{cc}x"& y"\end{array}\right]\end{array}$$

There is one further transformation. The coordinates returned at this point are normalised to lie in $[-1,1]$. The screen, however, is a rectangle of size WIDTH by HEIGHT. So the coordinates are transformed to screen coordinates via the transformation:

$$\begin{array}{rl}x"& \mapsto WIDTH(x"+1)/2\\ y"& \mapsto HEIGHT(y"+1)/2\end{array}$$

For good measure the $z$–coordinate ($z"$ in the above) is multiplied by $10$.

9 Saving the Result

What if instead of saving the matrix you want to save the result? Here it gets a bit complicated. The most likely scenario is that you start with a vector of the form $(x,y,z)$. You figure out some matrix that you would like to apply to this vector. You want to store the result of the transformation, perhaps to avoid doing the same computation every frame.

What should be saved? The answer depends on how you intend to reuse the saved data. A likely answer is that you will feed it back into the process from the start again. But here we have a possible problem. The right thing to save is $\stackrel{\rightharpoonup }{v}M$: the result of applying the matrix and before the perspective projection takes place. This is because that projection will always be done, it is always the same, and you only want it done once. So caching it makes no sense and only destroys information that, in an intermediate step, you should keep. Thus we save $\stackrel{\rightharpoonup }{v}M$. But this is a vector of length $4$ and we need to feed a vector of length $3$ into the system. Thus given a vector of length $4$, say $\stackrel{\rightharpoonup }{v}=(x,y,z,w)$, we need to find a vector of length $3$, say $\stackrel{\rightharpoonup }{v}\text{'}=(x\text{'},y\text{'},z\text{'})$, with the property that the final point produced by $(x\text{'},y\text{'},z\text{'})$ is the same as if we started with $(x,y,z,w)$.

Recall that the $3$–vector gets promoted to $\widehat{\stackrel{\rightharpoonup }{v}\text{'}}=(x\text{'},y\text{'},z\text{'},1)$. Then we apply some (new) matrix to it to get $\widehat{\stackrel{\rightharpoonup }{v}\text{'}}M$ and we want to compare this to $\stackrel{\rightharpoonup }{v}M$. But this is not the end of the story. At this point we divide by the fourth coordinate. When this happens, we lose information. If two vectors differ by a (non-zero) scale factor then they will be the same after dividing through. So we don't need to choose $\stackrel{\rightharpoonup }{v}\text{'}$ so that $\widehat{\stackrel{\rightharpoonup }{v}\text{'}}M$ and $\stackrel{\rightharpoonup }{v}M$ are the same, they can differ by a scale factor. Then if $\widehat{\stackrel{\rightharpoonup }{v}\text{'}}M$ and $\stackrel{\rightharpoonup }{v}M$ can differ by a scale factor, so can $\widehat{\stackrel{\rightharpoonup }{v}\text{'}}$ and $\stackrel{\rightharpoonup }{v}$. Since we know that $\widehat{\stackrel{\rightharpoonup }{v}\text{'}}$ has a $1$ in the fourth place, this scale factor must be the fourth place of $\stackrel{\rightharpoonup }{v}$. That is to say that as $\stackrel{\rightharpoonup }{v}=(x,y,z,w)$ and $\widehat{\stackrel{\rightharpoonup }{v}\text{'}}=(x\text{'},y\text{'},z\text{'},1)$, so we must have $\stackrel{\rightharpoonup }{v}=w\widehat{\stackrel{\rightharpoonup }{v}\text{'}}$ and thus $x\text{'}=x/w$ and similar.

Thus when saving the result of a matrix, we apply the matrix to the augmented vector and save the projected result.

Since Codea doesn't allow us to multiply vec4 objects by matrices, this means that we have to use the translate trick from earlier. So our code would be something like the following.

function applyTransformation(v,m)
    m = m:translate(iv.x,iv.y,iv.z)
    return = vec3(m[13],m[14],m[15])/m[16]
end

10 More Matrices

In the above we've only talked about the model matrix. This encodes the transformation from an object's internal coordinates to the ambient "world" coordinates. There are more transformations involved before a point is actually drawn on the screen. The next transformation is the viewMatrix. The idea behind this transformation is to place the viewer in the scene. So you imagine yourself standing at a particular point (and by "standing at a point" I really mean that your eyes are at this point), looking at some point, and a particular way up. This defines a new set of coordinates with your head as the origin, "up" as the $y$–direction and the vector to the point you are looking at as the $z$–direction (well, the minus $z$–direction). The $x$–direction is then on your right.

As the main purpose of this matrix is this purpose (setting the scene) then the "proper" way to set this is via the camera function. But as with the model matrix, it can be set to anything.

Lastly, there is the projection matrix. After the 3D scene has been set, it needs to be projected onto a 2D screen. The image to have here is of holding up the screen in front of you and drawing on it what you see through it, much as I described earlier. In the implementation, it is rather that the screen is fixed in place and we have to move the world around so that what is seen through the screen is what is wanted. Included in the "drawing on the screen" part are the "ignore stuff off-screen" and the "ignore stuff too close and too far away" parts.

Again, there are "standard" ways to set up this matrix.

In actual fact, the three matrices so described could be combined into one. The reason to separate them is to make it easier to manipulate the transformation by "standard" means. Moreover, it makes it easier in another regard in that the order of working on the three matrices does not matter as they are not combined until the end. But if wanting to do "strange" things, it isn't necessary to prefer one over another. In the above discussion, the matrix talked about should be thought of as representing the combination of these three transformations.

11 Reversing the Flow

The above all relates to understanding how to get something on to the screen. There are situations in which one might want to get something off the screen. That is, to transform something from screen coordinates back into world coordinates. The most likely situation for this is taking the coordinates of a touch and transforming it back into world coordinates.

The first thing to realise is that this is impossible. The screen is two dimensional and space is three dimensional. Information is lost and cannot be recovered. A point on the screen corresponds not to a point in space but to a line. We should not think of pointing at but rather pointing along.

Getting that line is simply a matter of reversing the process from world to screen. We start with a point on the screen, say $\stackrel{\rightharpoonup }{t}$. This is in screen coordinates so we need to normalise so that the ranges of $x$ and $y$ values are $[-1,1]$. This is straightforward.

$$\begin{array}{rl}x& =2t_x/WIDTH-1\\ y& =2t_y/HEIGHT-1\end{array}$$

Now we need a $z$. This also should be in the range $[-1,1]$. It may be that there is a particular value that we want to use so we will leave this free for now.

Then we promote this to a $4$–vector: $(x,y,z,1)$. The next step is to solve for $\stackrel{\rightharpoonup }{v}M=(x,y,z,1)$. Finally, we convert the result back to a $3$–vector by dividing by the fourth coordinate.

To get the ray we do this for two different $z$–values and take the line through them both.

The problem with this method is that it is very prone to numerical error. The matrix $M$ will typically be almost singular meaning that minor changes in the initial conditions can lead to large changes in the result. Inverting the matrix $M$ will exacerbate these problems, but even with a more robust solver there will still be sensitive dependence on initial conditions.

Instead, what is better is to break the problem into pieces. The most likely first step is the question "Was this object touched?". This can be tested in screen coordinates. The object's basic shape can be computed by forward projection of its coordinates and the touch can be tested for being inside this shape. There are potential disadvantages with this: it ignores the fact that an object might be partially behind another, and the "shadow" might be quite complicated. However, these are only potential disadvantages. The system can check objects in the right order if it needs to (but there can be advantages in not having to check in this order), and touches will never be so accurate that the exact shape has to be used: an approxiation will suffice.

The second part of the problem does involve reversing the transformation as once the object knows it has been touched then it might want to use that information to act. But remember that we lose information because we have gone from three to two dimensions. One remedy is to add back a third dimension. An alternative is to ensure that we start with just two to begin with.

This is done by having the object declare a "plane of movement". This is a (translated) plane in space. The purpose is to find the right touch point on that plane rather than anywhere in space.

A plane can be specified by giving three points on it, or one point on it and two directions within it. In this second formulation an arbitrary point is of the form $\stackrel{\rightharpoonup }{p}(s,t)=\stackrel{\rightharpoonup }{o}+s\stackrel{\rightharpoonup }{u}+t\stackrel{\rightharpoonup }{v}$. Now we apply the transformation matrix, $M$, to get $\stackrel{\rightharpoonup }{p}(s,t)M$. From this, we discard the third component and divide by the fourth. Let us write $M$ as four column vectors, $M=\left(\begin{array}{cccc}{\stackrel{\rightharpoonup }{m}}_1& {\stackrel{\rightharpoonup }{m}}_2& {\stackrel{\rightharpoonup }{m}}_3& {\stackrel{\rightharpoonup }{m}}_4\end{array}\right)$. Then the result of the transformation is:

$$\left[\begin{array}{cc}\frac{\stackrel{\rightharpoonup }{p}(s,t){\stackrel{\rightharpoonup }{m}}_1}{\stackrel{\rightharpoonup }{p}(s,t){\stackrel{\rightharpoonup }{m}}_4}& \frac{\stackrel{\rightharpoonup }{p}(s,t){\stackrel{\rightharpoonup }{m}}_2}{\stackrel{\rightharpoonup }{p}(s,t){\stackrel{\rightharpoonup }{m}}_4}\end{array}\right]$$

It turns out that this can be implemented by a $3\times 3$–matrix. That is, there is a $3\times 3$–matrix, say $A$, such that the above transformation is obtained by applying $A$ to $(s,t,1)$ and then dividing by the third coordinate. The advantage of this is that if we choose $\stackrel{\rightharpoonup }{u}$ and $\stackrel{\rightharpoonup }{v}$ well then $A$ has a much better chance of being non-singular than $M$ did.

The formula for $A$ is not complicated: it depends on $M$ and the vectors chosen to specify the plane:

$$\stackrel{\rightharpoonup }{p}(s,t)M=(\stackrel{\rightharpoonup }{o}+s\stackrel{\rightharpoonup }{u}+t\stackrel{\rightharpoonup }{v})\left[\begin{array}{ccc}{\stackrel{\rightharpoonup }{m}}_1& {\stackrel{\rightharpoonup }{m}}_2& {\stackrel{\rightharpoonup }{m}}_4\end{array}\right]=(s,t,1)\left[\begin{array}{c}\stackrel{\rightharpoonup }{u}\\ \stackrel{\rightharpoonup }{v}\\ \stackrel{\rightharpoonup }{o}\end{array}\right]\left[\begin{array}{ccc}{\stackrel{\rightharpoonup }{m}}_1& {\stackrel{\rightharpoonup }{m}}_2& {\stackrel{\rightharpoonup }{m}}_4\end{array}\right]$$

The best choices for $\stackrel{\rightharpoonup }{u}$ and $\stackrel{\rightharpoonup }{v}$ will be to make this transformation as far from singular as possible. To that end, it is useful to be able to compute the vector that points along the touch ray at the given touch point. Then among the available choices, $\stackrel{\rightharpoonup }{u}$ and $\stackrel{\rightharpoonup }{v}$ should be as close as possible to normal to this vector.

Fortunately, that vector can be computed from the touch position and the forward matrix. This is because the partial derivatives of the full transformation are given by formulae like the following, wherein $X$ and $Y$ are the normalised screen coordinates and $\stackrel{\rightharpoonup }{q}=(x,y,z,1)$.

$$\frac{\partial X}{\partial x}=\frac{1}{\stackrel{\rightharpoonup }{q}{\stackrel{\rightharpoonup }{a}}_4}(a_{11}-X{a}_{41})$$

And the vector along the touch ray is the kernel of the resulting matrix, which can be found without knowing $\stackrel{\rightharpoonup }{q}$ and using the normalised touch coordinates for $X$ and $Y$.

To sum up this section, reversing the transformation fully is not recommended due to the high likelihood of numerical error. But using information that can be computed, it is possible to find a plane in space such that the transformation onto that plane is more robust and so can be inverted. Thus the processing when a touch event occurs should be something like the following.

1. An object tests the touch against its "shadow" on the screen to see if it has been touched.

2. The object chooses a "best plane" using the "touch ray".

3. The object converts the touch data to useful data using the "best plane".

As an example, a cube might use whichever of its faces is most "towards" the screen

12 Normals

At the beginning, we made a distinction between a model's own coordinates and the world coordinates. That is, that an object might have its own natural coordinates which are different to those of the world that it is in. For many aspects of rendering an object the flow of information is purely one way: from the model's perspective to the world's perspective. But some aspects require the model knowing something about the world around it. One of these is lighting.

Let us imagine a simple situation: we are lighting our object as if by the sun. So the light source is far, far away. Far enough that we can assume that the light rays reaching the object are parallel. Far enough also that we can assume that there is no variation in intensity. So the light is completely specified by a direction and an intensity.

Now consider an object illuminated by this light. Exactly how this object appears depends on the material that the object is made off. A shiny surface will reflect the light in a single direction, a matt surface will reflect it in all directions. For simplicity, let us assume that it is a matt surface and that the light is reflected evenly in all directions. This means that when you look at a particular point on the object then it appears the same no matter where you are looking from.

In order to compute the effect of the light we just need to compute the amount of light falling on it. We imagine a flat surface (technically, all our objects are built from flat triangles so this is actually a true assumption, but even in theory then we can approximate our surface by a flat surface near a given point). We want to compute how much light falls on this surface. To do this, it is easiest to imagine light as a stream of particles. These particles are moving in the direction of the light at a constant velocity. The number of particles that hit the surface in a given time depends on the area of the surface as seen from the light direction.

That is, the actual area of the surface doesn't matter: it is the area as seen by the light that matters.

Let's draw a picture to illustrate it one dimension down. The black lines all receive the same amount of light in a given time because their size in the direction of the light is the same.

We're actually in the opposite situation. We can assume that the pieces of the object are all the same size (this is because the fragment shader slices them into tiny pieces) and so the question is as to what the area of these pieces is as seen by the light. To answer that, we need to measure the angle of the surface to the light.

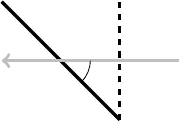
Let us suppose that it is at angle $\theta$ to the light. Then the area as seen by the light is $\sin (\theta )$ times the actual area. We can compute this directly (i.e., without needing to know $\theta$) if we know the unit normal vector to the surface. Providing both are of length $1$, if $\stackrel{\rightharpoonup }{n}$ is the normal and $\stackrel{\rightharpoonup }{l}$ the light vector then we have $\stackrel{\rightharpoonup }{n}\cdot \stackrel{\rightharpoonup }{l}=\sin (\theta )$.

Thus the amount of light landing on a segment of the surface is $\stackrel{\rightharpoonup }{n}\cdot \stackrel{\rightharpoonup }{l}$. We can use this to adjust the brightness of the object at that point. We assume that a piece of the object that is at right angles to the light (i.e., is "face on") is fully illuminated and shown at its natural colour. A piece of the object that is "side on" has no light from the light source so should be dark. A piece of the object that is facing away from the light source should also be dark. Thus we want to use $\stackrel{\rightharpoonup }{n}\cdot \stackrel{\rightharpoonup }{l}$ for when the piece of the object is facing the light, and $0$ when facing away. Fortunately, the value of $\stackrel{\rightharpoonup }{n}\cdot \stackrel{\rightharpoonup }{l}$ tells us also when the object is facing towards or away from the light: it is positive if towards and negative if away.

(There are two slight complications here. We are assuming that for any piece of the object there is a definite "side" to it. Namely, one side will be visible and one side hidden. This is true for most solid shapes, but there are strange surfaces where it fails. The other complication is that the light might be obscured by some other object. Resolving this issue is beyond this article.)

So for a point on the surface we compute $\stackrel{\rightharpoonup }{n}\cdot \stackrel{\rightharpoonup }{l}$ and use that to dim the light. If it is negative, we dim the light completely. Thus our light factor is actually $\max (0,\stackrel{\rightharpoonup }{n}\cdot \stackrel{\rightharpoonup }{l})$. Note that we might not want to dim the colour of our object completely. If we assume some ambient light, the formula will be something like: $a+(1-a)\max (0,\stackrel{\rightharpoonup }{n}\cdot \stackrel{\rightharpoonup }{l})$ where $a$ is the ambient light and $1-a$ the remaining factor.

In order to make use of this, we need to augment our object data by adding in the normal vectors at each vertex. This can often be done quite simply when the object is created.

However, there is a serious complication which is particularly important if the object is to be used more than once, or if the transformation from the model's space to the world space can change. This is that the normals in the model's space and the normals in the world space are not necessarily the same.

To see why, consider an object that is a circle in its own coordinate system but which becomes an ellipse when transported into the world. In its own coordinate system, the normal vector at a point is simply the vector pointing straight out from the centre. But this is no longer normal when transformed to the world's coordinate system.

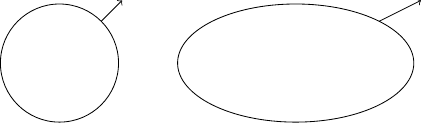
The problem is that "being normal to a surface" is a fragile condition. It depends on angles, and angles are not always preserved by transformations. On the other hand, "being tangent to a surface" is preserved by transformations. So one way to compute the world's normal would be store tangential vectors and use them to compute the normal after they have been transformed. The problem with this is that it involves storing twice the amount of information (we need two tangent vectors for each point) and doing two lots of transformations, so more memory is used and more time in computation.

Nonetheless, we can use the fact that the tangent vectors remain tangential to get a quick way to compute the normal. Suppose that our transformation from model space to world space is given by the affine transformation $\stackrel{\rightharpoonup }{x}\mapsto A\stackrel{\rightharpoonup }{x}+\stackrel{\rightharpoonup }{b}$. Then a tangent vector, say $\stackrel{\rightharpoonup }{v}$, is transformed to $A\stackrel{\rightharpoonup }{v}$. This is because $\stackrel{\rightharpoonup }{v}$ is actually the tangent vector at a point, say $\stackrel{\rightharpoonup }{p}$, so when we compute what it becomes we look at what happens to $\stackrel{\rightharpoonup }{v}+\stackrel{\rightharpoonup }{p}$ and subtract what happens to $\stackrel{\rightharpoonup }{p}$:

$$(A(\stackrel{\rightharpoonup }{v}+\stackrel{\rightharpoonup }{p})+\stackrel{\rightharpoonup }{b})-(A\stackrel{\rightharpoonup }{p}+\stackrel{\rightharpoonup }{b})=A\stackrel{\rightharpoonup }{v}.$$

Suppose that ${\stackrel{\rightharpoonup }{v}}_1$ and ${\stackrel{\rightharpoonup }{v}}_2$ are tangent to the object at point $\stackrel{\rightharpoonup }{p}$ in model space. Let us write ${\stackrel{\rightharpoonup }{n}}_m$ ($m$ for "model") for the normal vector at $\stackrel{\rightharpoonup }{p}$ in the model's space.

Then $A{\stackrel{\rightharpoonup }{v}}_1$ and $A{\stackrel{\rightharpoonup }{v}}_2$ are tangent to $A\stackrel{\rightharpoonup }{p}+\stackrel{\rightharpoonup }{b}$ in world space. We want to find the normal, and this is a vector, say ${\stackrel{\rightharpoonup }{n}}_w$ ($w$ for "world"), which is at right angles to both $A{\stackrel{\rightharpoonup }{v}}_1$ and $A{\stackrel{\rightharpoonup }{v}}_2$. That is, it satisfies $(A{\stackrel{\rightharpoonup }{v}}_1)\cdot {\stackrel{\rightharpoonup }{n}}_w=0$ and $(A{\stackrel{\rightharpoonup }{v}}_2)\cdot {\stackrel{\rightharpoonup }{n}}_w=0$.

Now for two vectors, say $\stackrel{\rightharpoonup }{x}$ and $\stackrel{\rightharpoonup }{y}$, and a matrix, say $B$, we have the following neat identity: $(B\stackrel{\rightharpoonup }{x})\cdot \stackrel{\rightharpoonup }{y}=\stackrel{\rightharpoonup }{x}\cdot (B^{\top }\stackrel{\rightharpoonup }{y})$ where $B^{\top }$ denotes the transpose of $B$ (this is $B$ reflected in the main diagonal).

So we're looking for a vector ${\stackrel{\rightharpoonup }{n}}_w$ such that ${\stackrel{\rightharpoonup }{v}}_1\cdot (A^{\top }{\stackrel{\rightharpoonup }{n}}_w)=0$ and ${\stackrel{\rightharpoonup }{v}}_2\cdot (A^{\top }{\stackrel{\rightharpoonup }{n}}_w)=0$. This means that $A^{\top }{\stackrel{\rightharpoonup }{n}}_w$ is at right angles to both ${\stackrel{\rightharpoonup }{v}}_1$ and ${\stackrel{\rightharpoonup }{v}}_2$. These identities are happening in the model's space: the $A^{\top }$ has taken us back from the world space to the model's space. And a vector that is at right angles to ${\stackrel{\rightharpoonup }{v}}_1$ and ${\stackrel{\rightharpoonup }{v}}_2$ is ${\stackrel{\rightharpoonup }{n}}_m$, the normal vector at $\stackrel{\rightharpoonup }{p}$.

We therefore want ${\stackrel{\rightharpoonup }{n}}_w$ such that $A^{\top }{\stackrel{\rightharpoonup }{n}}_w={\stackrel{\rightharpoonup }{n}}_m$. If $A$ (whence $A^{\top }$) is invertible, we can invert it to solve this as ${\stackrel{\rightharpoonup }{n}}_w=(A^{\top }{)}^{-1}{\stackrel{\rightharpoonup }{n}}_m$.

Now, the Golden Rule of linear algebra is: Never invert a matrix. There are always simpler ways to solve a problem than inverting a matrix. Here, though, the Golden Rule might be considered violable simply because we are going to want to compute $(A^{\top }{)}^{-1}{\stackrel{\rightharpoonup }{n}}_m$ for every vertex in the mesh and there could be a large number of these. We can make these computations cheap by computing $(A^{\top }{)}^{-1}$ once at the start.

Better, though, is to avoid computing $(A^{\top }{)}^{-1}$ directly. Often the transformation from object space to world space is built out of simple pieces, such as rotations and scalings, and as we build up $A$ from these pieces it is easy to build up $(A^{\top }{)}^{-1}$ from similar pieces. Then we pass $(A^{\top }{)}^{-1}$ directly in to the shader and it doesn't have to compute it directly from $A$.

There is yet another complication. The matrix used for computing normals is just the linear part of the transformation from model space to world space. We need to discard the translation part. Recall that we implement $3$–dimensional affine transformations as $4\times 4$–matrices. It is easiest to build $(A^{\top }{)}^{-1}$ also as a $4\times 4$–matrix simply because Codea is geared up for working with $4\times 4$–matrices and not $3\times 3$. When we build the $4\times 4$–matrix then the $3\times 3$ one is the upper left corner.

13 Complete Code

We end with some (hopefully) illustrative code. In my library I have general matrix and vector types and some of this code could be added to them.

function setup()
    --displayMode(FULLSCREEN_NO_BUTTONS)
    cube = mesh()
    corners = {}
    for l=0,7 do
        i,j,k=l%2,math.floor(l/2)%2,math.floor(l/4)%2
        table.insert(corners,{vec3(i,j,k),color(255*i,255*j,255*k)})
    end
    vertices = {}
    colours = {}
    local u
    for l=0,2 do
        for i=0,1 do
            for k=0,1 do
                for j=0,2 do
                    u = (i*2^l + ((j+k)%2)*2^((l+1)%3)
                        + (math.floor((j+k)/2)%2)*2^((l+2)%3)) + 1
                    table.insert(vertices,corners[u][1])
                    table.insert(colours,corners[u][2])
                end
            end
        end
    end
    cube.vertices = vertices
    cube.colors = colours

    parameter("x",-5,5,0)
    parameter("y",-5,5,0)
    parameter("z",-10,10,0)
    watch("mid")
    watch("mat")
    watch("dbg")
    cubepos = vec3(0,0,1)
    watch("cubepos")
end

function draw()
    background(40, 40, 50)
    noSmooth()
    noStroke()
    fill(0, 255, 238, 255)
    ellipse(CurrentTouch.x,CurrentTouch.y,15)
    resetMatrix()
    perspective(40, WIDTH/HEIGHT)
    camera(0,0,10,  0,0,0,  0,1,0)
    mat = modelMatrix()*viewMatrix()*projectionMatrix()
        pushMatrix()
        translate(x,y,z)
        cube:draw()
        popMatrix()
        pushMatrix()
        cubeMatrix = modelMatrix()*viewMatrix()*projectionMatrix()
        translate(cubepos.x,cubepos.y,cubepos.z-1)
        cube:draw()
        popMatrix()
end

function touched(touch)
    local tc = screentoplane(touch,
                  vec3(0,0,1),
                  vec3(1,0,0),
                  vec3(0,1,0),
                  cubeMatrix)
    if touch.state == BEGAN then
        if tc.x > cubepos.x and tc.x < cubepos.x + 1 and
            tc.y > cubepos.y and tc.y < cubepos.y + 1 then
                cubetouch = tc - cubepos
        else
            cubetouch = false
        end
    else
        if cubetouch then
            cubepos = tc - cubetouch
        end
    end
end

function converttouch(z,t,A)
    A = A or modelMatrix() * viewMatrix() * projectionMatrix()
    t = t or CurrentTouch or vec2(0,0)
    z = z or 0
    local m = cofactor4(A)
    local ndc = {}
    local a
    ndc[1] = (t.x/WIDTH - .5)*2
    ndc[2] = (t.y/HEIGHT - .5)*2
    ndc[3] = z
    ndc[4] = 1
    a = applymatrix4(ndc,m)
    if (a[4] == 0) then return end
    a = vec3(a[1], a[2], a[3])/a[4]
    return a
end

function getzlevel(v,A)
    A = A or modelMatrix() * viewMatrix() * projectionMatrix()
    v = v or vec3(0,0,0)
    local u = applymatrix4(vec4(v.x,v.y,v.z,1),A)
    if u[4] == 0 then return end
    return u[3]/u[4]
end

function applymatrix4(v,m)
    local u = {}
    u[1] = m[1]*v[1] + m[5]*v[2] + m[09]*v[3] + m[13]*v[4]
    u[2] = m[2]*v[1] + m[6]*v[2] + m[10]*v[3] + m[14]*v[4]
    u[3] = m[3]*v[1] + m[7]*v[2] + m[11]*v[3] + m[15]*v[4]
    u[4] = m[4]*v[1] + m[8]*v[2] + m[12]*v[3] + m[16]*v[4]
    return u
end

function cofactor4(m)
    local rm = matrix()
    local sgn,l
    local fm = {}
    for k=1,16 do
        fm = {}
        l = math.floor((k-1)/4) + 1 + 4*((k-1)%4)
        sgn = (-1)^(math.floor((k-1)/4))*(-1)^((k-1)%4)
        for j=1,16 do
            if j%4 ~= k%4
                and math.floor((j-1)/4) ~= math.floor((k-1)/4)
                then
                    table.insert(fm,m[j])
            end
        end
        rm[l] = sgn*Det3(fm)
    end
    return rm
end

function Det3(t)
    return t[1]*t[5]*t[9]
         + t[2]*t[6]*t[7]
         + t[3]*t[4]*t[8]
         - t[3]*t[5]*t[7]
         - t[2]*t[4]*t[9]
         - t[1]*t[6]*t[8]
end

function applymatrix3(v,m)
    local u = {}
    u[1] = m[1]*v[1] + m[4]*v[2] + m[7]*v[3]
    u[2] = m[2]*v[1] + m[5]*v[2] + m[8]*v[3]
    u[3] = m[3]*v[1] + m[6]*v[2] + m[9]*v[3]
    return u
end

function cofactor3(m)
    local rm = {}
    local sgn,l
    local fm = {}
    for k=1,9 do
        fm = {}
        l = math.floor((k-1)/3) + 1 + 3*((k-1)%3)
        sgn = (-1)^(math.floor((k-1)/3))*(-1)^((k-1)%3)
        for j=1,9 do
            if j%3 ~= k%3
                and math.floor((j-1)/3) ~= math.floor((k-1)/3)
                then
                    table.insert(fm,m[j])
            end
        end
        rm[l] = sgn*Det2(fm)
    end
    return rm
end

function Det2(t)
    return t[1]*t[4] - t[2]*t[3]
end

function __planetoscreen(o,u,v,A)
    A = A or modelMatrix() * viewMatrix() * projectionMatrix()
    o = o or vec3(0,0,0)
    u = u or vec3(1,0,0)
    v = v or vec3(0,1,0)
    -- promote to 4-vectors
    o = vec4(o.x,o.y,o.z,1)
    u = vec4(u.x,u.y,u.z,0)
    v = vec4(v.x,v.y,v.z,0)
    local oA, uA, vA
    oA = applymatrix4(o,A)
    uA = applymatrix4(u,A)
    vA = applymatrix4(v,A)
    return { uA[1], uA[2], uA[4],
             vA[1], vA[2], vA[4],
             oA[1], oA[2], oA[4]}
end

function screentoplane(t,o,u,v,A)
    A = A or modelMatrix() * viewMatrix() * projectionMatrix()
    o = o or vec3(0,0,0)
    u = u or vec3(1,0,0)
    v = v or vec3(0,1,0)
    t = t or CurrentTouch
    local m = __planetoscreen(o,u,v,A)
    m = cofactor3(m)
    local ndc = {}
    local a
    ndc[1] = (t.x/WIDTH - .5)*2
    ndc[2] = (t.y/HEIGHT - .5)*2
    ndc[3] = 1
    a = applymatrix3(ndc,m)
    if (a[3] == 0) then return end
    a = vec2(a[1], a[2])/a[3]
    return o + a.x*u + a.y*v
end

function screennormal(t,A)
    A = A or modelMatrix() * viewMatrix() * projectionMatrix()
    t = t or CurrentTouch
    local u,v,w,x,y
    u = vec3(A[1],A[5],A[9])
    v = vec3(A[2],A[6],A[10])
    w = vec3(A[4],A[8],A[12])
    x = (t.x/WIDTH - .5)*2
    y = (t.y/HEIGHT - .5)*2
    u = u - x*w
    v = v - y*w
    return u:cross(v)
end

14 Afterword

This article, with the exception of this afterword, was written entirely on the iPad in LaTeX using TeX Writer. This made it easy to include code snippets from Codea programs and screenshots. TeX Writer produces a PDF which can be downloaded. The resulting TeX document was converted to a suitable format for including in my website (MarkdownExtra+iTeX) by a newer version of the internet class.

Codea is an iPad application for programming animations and simulations in lua. It has an active forum. Comments about this post should be left there. The final program above can also be downloaded.