Contents
In the summer of 2020 I gave a talk in the Talk Math With Your Friends online series with the title From Clocks to Categories. The talk had two strands to it:
-
There is Category Theory in school level Mathematics.
-
So what?
In this post I want to go into a bit more detail on the first of these and explain the Mathematics behind the things that I mentioned in my talk. If you know about category theory already, you can think of this as a source of examples for if you get asked to explain it to someone. If you don't know about category theory, this will hopefully give you a flavour of it with non-scary examples.
One thing that needs saying at the outset is that my goal is to find examples where the categorical viewpoint is already there. By its nature as a foundational theory of Mathematics, I can recast all of school Mathematics in a categorical framework. But most of the time that involves bringing in additional structure. For example, if I think about the field structure of the real numbers then I can consider as an object in the category of fields. However, without knowledge of other fields then this isn't really school Mathematics anymore. So I want to find aspects of category theory that are already present and just need a little changing of perspective or perhaps a small additional idea to reveal them.
1 Why Category Theory?
Let me briefly explain why I'm interested in finding category theory in school Mathematics. Many years ago, back when I was an academic, a question was asked on MathOverflow about when to teach category theory. I gave an answer, and as part of that answer I wrote:
I believe that category theory is an excellent way to understand and express mathematical concepts. I find in my own work that, time and time again, when I express my ideas using categorical language then it makes them clearer both to me and to others. Believing this, as I do, why on earth would I want to deprive my students of the same benefits?
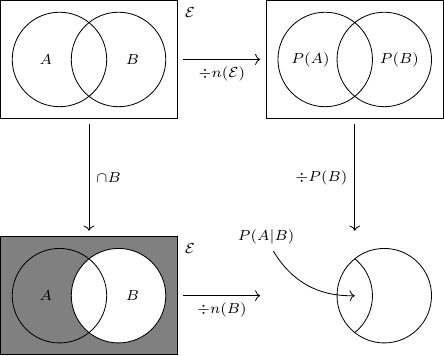
As I said, this was when I was an academic and giving lectures to undergraduates. When I switched to teaching in a school I did think that it would be a bit of a stretch to include category theory in my day to day lessons. But then one day I was trying to explain about conditional probability and I drew on a board the diagram in Figure 1. It felt like a diagram straight out of a text book on category theory.
Before I go further, I should explain that I do not use the terminology of category theory when teaching. Rather it is that I find myself, time and time again, using the language of category theory.
2 Category Theory: the Basics
I've described category theory at times as being Ubuntu Mathematics: a thing is what it is because of how it relates to other things. So we don't examine a thing in isolation but we examine it in a context of similar things.
Thus the aspect of category theory that I find foundational is that it puts the focus on the relationships between things rather than the things themselves. So in all of this, the goal is to lift the focus of attention ever higher in the hierarchy.
With that in mind, here are the basic definitions of terms that I'll be using in this article. I'll separate out the definitions a bit so that I can provide a running commentary, thus the early definitions are not complete.
A category consists of objects and arrows.
An arrow has a source (or domain) and target (or codomain), both of which are objects in the category.
A more common name for the arrows is morphisms, but as my intention is that this makes sense to someone who hasn't heard of category theory, I'll use the more normal-sounding "arrow" instead.
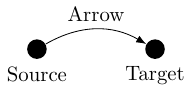
We think of the arrow as going from its source to its target, but it actually isn't necessarily the case that an arrow fits that mould quite so neatly. Actual examples will come later, but there are various pictures that have proven to be useful to have in mind. The "arrow" terminology comes in useful with pictures like Figure 2.
"Objects as blobs" is quite a useful point of view in category theory: we try not to look too closely at the objects themselves.
If you know a bit about the history of category theory, you might be expecting me to talk about classes and sets here. I shan't. If you know it, great. If you don't know it, you probably aren't bothered by it and I don't want to try to cover everything here.
On with the definitions.
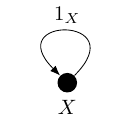
Every object has a special arrow called the identity arrow, which has source and target that object. For an object , we will write this as or (particularly if has other meanings in context).
In terms of pictures, this might look like Figure 3
The one piece of structure that categories always have is that one can compose arrows providing they line up correctly.
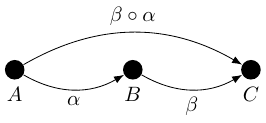
If the target of one arrow is the source of a second then these two arrows can be composed (in the obvious order) to produce a third.
Figure 4 is the picture for this.
Notice that I'm writing composition in "inside-out" order. This is a convention, and others will write them in "left-to-right" order. I once wrote a paper in which I made it possible to easily switch between these just in case the referee asked for it (they didn't).
Composition satisfies two basic rules:
-
Associativity:
-
Identities are identities:
Notice that in that second one, the identities are different since one is at the source of and the other at its target. In those rules, I've tacitly assumed that the various compositions make sense, for example that the target of is the source of .
3 Examples of Categories in School Mathematics
Here, I'll gather the examples of categories from school Mathematics that I'll use in the rest.
3.1 Clock Arithmetic
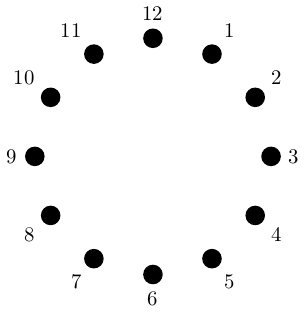
This was my first example in the Talk Math With Your Friends talk. There are actually several categories here depending on how finely you divide time.
A clock category has:
-
Object: times
-
Arrows: durations
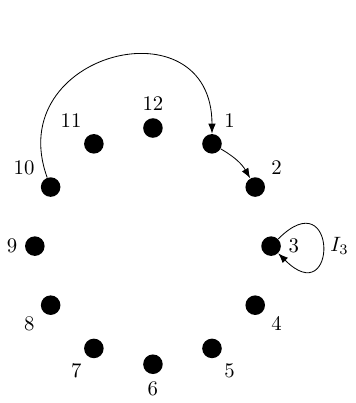
The one I gave in the talk was based on hourly divisions. More precisely, the objects were hours on a clock. So we can draw the objects of this category very neatly as a clock, as in Figure 5.
The arrows are the durations, which are a little harder to draw if we try to draw all of them. Rather, let us draw a representative few in Figure 6.
I feel that this is a simple enough example that I don't need to go into great detail as to proving that this makes a category. Rather, I'll list some half-baked thoughts on what the categorical viewpoint brings to this example.
-
It separates out the related but often conflated notions of time and duration.
Times are measures of position. By focussing on hours on the clock, we can't even talk about "earlier" or "later" for such times since we don't know if o'clock is earlier or later than o'clock. There are situations that make either one true. In particular, we can't add or subtract times and we certainly can't multiply them.
Durations are more algebraic. We can add and subtract durations. Although we can't multiply durations, we can consider multiples of the same duration (so, there's a secret –action here).
-
It emphasises the distinction between abstract durations and concrete durations.
By a concrete duration, I mean something like " hours after o'clock". This is a specific arrow. An abstract duration would be just " hours". So it's a duration looking for a source1.
1That this makes sense is a special property of this category, not all categories have the ability to detach their arrows in this fashion.
This could be used to break down the passage from the concrete concepts of arithmetic to the abstract into smaller pieces.
-
It brings out the contextual element of arithmetic.
What is ? If we regard these as concrete durations, we have to expand this to "What do we get if we wait hours after o'clock and then hours after that?" But even that is ambiguous! There are two possible answers depending on whether what we want is the time after that wait or the total duration. If all we care about is the destination, the answer is o'clock. If all we care about is the duration, the answer is hours. But both of those are partial answers. The full answer is that we get the duration (arrow) of hours after o'clock, and the end time (target) of this arrow is o'clock.
-
It means we no longer have to make that weird statement when introducing modular arithmetic about how we regard o'clock as . We don't. It is a duration of hours that has the same target as a duration of hours.
3.2 Sequences
There are many categories of sequences. The one that I'm going to use later on is that of arithmetic or linear sequences.
The category of Arithmetic Sequences has:
-
Objects: arithmetic sequences
-
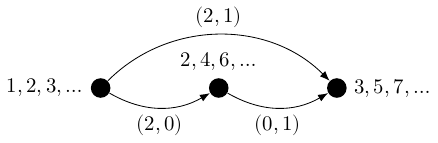
Arrows: an arrow from one sequence to another, say from to , is a pair of numbers with the property that for each , .
As with the clock category, the arrows have a description that is separate to their source and target so it is tempting to talk about a pair as a generic arrow. One thing that this doesn't capture is that the behaviour of these arrows is subtly different on constant sequences versus non-constant ones. There is a single arrow from any non-constant sequence to any other given sequence. There are no arrows from constant sequences to non-constant sequences. There are many arrows between two constant sequences.
I said at the outset that I wanted to reveal structure that was already in place rather than impose new structure on an existing framework. When I started thinking about this category then I felt that the arrows were an extra and that in school we tend to think about sequences individually. Then I thought a bit more and realised that while we tend not to think about arrows between arbitrary sequences, we do think about arrows from a very specific sequence: the counting sequence.
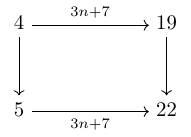
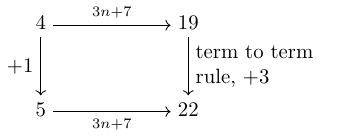
A common question for an arithmetic sequence, say , is to find a formula for its th term. One strategy for finding this is as follows: start by finding the common difference (in this case, ); consider the sequence formed by taking the multiples of that common difference (in this case, ); this differs from the original sequence by a constant shift (in this case, ). Put these together to get the th term rule (here, ). It is common to put these together into a table, as in Table 1.
What we are doing here is constructing an arrow from the sequence to our target sequence. Not only that, but we're doing it in two stages so we've constructed it as the composition of, in this case, followed by , as shown in Figure 7.
3.3 Shapes
Shapes are used all over school Mathematics, and using transformations makes it into an easy category.
The category of Shapes has:
-
Objects: subsets of
-
Arrows: transformations
Within this category, we can define various subcategories. A subcategory is quite a loose concept: we can throw out both objects and arrows. The main thing that we can't change is how to compose arrows.
Subcategories in common use are:
-
Restrict the objects:
-
Polygons
-
Curvy-linear shapes (imagine polygons but with arcs as well as straight lines)
-
Quadrilaterals
-
Triangles
-
-
Restrict the arrows:
-
Affine transformations
-
Shape-preserving (so, conformal affine transformations)
-
Shape and size-preserving (so, orthogonal affine)
-
Particularly when the arrows are reduced, we are concerned with classifying shapes that are related via an arrow. When the arrows are shape-preserving, we call these similar shapes. When the arrows are shape- and size-preserving, we call these congruent shapes.
The time when I find myself working most categorically here is when looking at similar shapes. I will often draw the two shapes with an arrow from one to the other labelled by the scale factor. This is to emphasise that the scale factor has a direction – it has a source shape (object) and a target shape (object). If we reverse the arrow, we have to take the inverse of the arrow and the scale factor changes accordingly.
3.4 Functions
Often, functions are presented as a key example of arrows in various categories. In this case, I want to present functions as the objects in a category.
The category of functions has:
-
Objects: functions
-
Arrows: pre and post composition by affine functions
When we think of an affine function, say , as an arrow then we need to include the information as to whether we are pre-composing or post-composing.
3.5 Numbers
There are lots of categories that involve numbers. The numbers can be objects (as here) or arrows (as in the clock category). With the numbers as objects, we can consider several different types of arrow which indicate what aspect of numbers we are considering.
Shifts:
-
Objects: some type of numbers (, , , )
-
Arrows: an arrow from to is labelled by (in the same number system) where
Scales or divisibility:
-
Objects: some type of numbers (, , , )
-
Arrows: an arrow from to is labelled by (in the same number system) where
Order:
-
Objects: some type of numbers (, , , )
-
Arrows: there is an arrow from to if
In this case, the arrow is unique if it exists.
The middle one is particularly interesting when one takes natural numbers because then there is an arrow from to if divides , so this is a natural place to discuss multiples, factors, and all matters relating to divisibility. This is also a situation where it is common to focus on the existence of an arrow separately to the arrow itself in that we often think about when divides without concerning ourselves as to what the multiplier is.
In all of the above categories of numbers then for almost all numbers, if we have an arrow then it is unique (the usual exception being ). We will also need the following category in which this is not true.
Arithmetic:
-
Objects: some type of numbers (, , , )
-
Arrows: an arrow from to is labelled by a pair where
4 Functors and Natural Transformations
If the focus of category theory is to shift the focus to the relationships between things, then it seems obvious that we should look at the relationships between categories themselves. Such things are called functors. These come in two types: covariant and contravariant. I'll explain these in Section 4.2.
I don't want to make this heavy on unnecessary definitions so I'll not give a formal definition of a functor. In short, it takes objects and arrows in one category to objects and arrows in a second category and "plays nicely" with the structure of each.
Now that we've introduced functors, the philosophy of category theory says that we should now think about how different functors are related. In other words, can we think of functors as objects in some new category and if so, what are the arrows? Unsurprisingly, the answer is "we can" and the arrows are called "natural transformations". I'll show these by example.
4.1 Sequences
A very simple source of examples of functors (and natural transformations) comes from considering sequences. Given a sequence, say , we can consider a particular term in that sequence, say . Sending a sequence to a term like this defines a functor from a category of sequences to a suitable category of numbers. All we have to do is make sure that our category of numbers has arrows to match those from our sequences. So if we're starting with our category of arithmetic sequences then we need to ensure that our arrows in the category of numbers includes ones of the form , such as our arithmetic category of numbers.
So we have functors like:
(While preparing the talk, I played around with getting emoji characters in the slides. They seemed to go down much better than the more usual mathfrak style in common use for functors.)
One thing that the categorical viewpoint emphasises here is the distinction between sequences and numbers, since they are in different categories. And in making that distinction then "taking the th term" perhaps becomes more of a deliberate act.
I've already mentioned the th term rule for a sequence as being an arrow to it from the "counting" sequence. Let's take a concrete example, the sequence , , , . This has th term rule , so categorically speaking we have:
Now let's apply some term functors to these sequences, and the arrow between them. Taking the th and th term functors we get two shadows of this arrow in a category of numbers:
A natural transformation means that we need an arrow between these two lines. What this turns out to mean is that we need arrows between the objects which make it a square, as in Figure 8.
The key properties of this square are as follows:
-
Each vertical edge depends only on that sequence and not on anything in the rest of the diagram.
-
Whichever route you take from top left to bottom right results in the same overall arrow.
Note that this means more than just you end up in the same place. The arrow obtained by composing the sides involved has to be the same as well.
It turns out that the right way to fill in the vertical arrows is to use the term to term rules for each sequence, as shown in Figure 9.
So term to term rules are examples of natural transformations (incidentally, there was nothing special about arithmetic sequences here).
4.2 Variance
Graphs are another example of functors and these illustrate the important concept of variance. Since arrows have a direction, it is sometimes the case that one wants to think of an arrow going in the opposite direction to its natural one. For example, with the category of natural numbers and arrows for divisibility, maybe we'd rather say that there is an arrow if is a multiple of . This is exactly the same as the original category except that we've reversed all the arrows. For such a simple thing, it has a remarkably broad impact.
The concept of variance comes in when we have a functor that ought to be defined by reversing the arrows in one of its categories (source or target) but we don't want to acknowledge that. In this case we say that the functor is contravariant. Ordinary functors are said to be covariant. Taking graphs of functions is a nice example of how these two behave.
We start with a category of functions on the reals. Our arrows will be composition by functions of the form with non-zero, but we have a choice as to whether to take pre-composition or post-composition so actually we have two categories, one for each option.
The functor assigns to a function its graph so our target category is a category of shapes in the plane. That is, for a function we end up with the shape:
What happens with arrows depends on which category we started with. Let's start with post-composition, so we have and . Then is related to by scaling by and then translation by in the –direction.
With pre-composition we have and . Again, we have that and are related by scaling by and translation by – this time in the –direction – but it is actually that is obtained from by scaling by and then translation by .
This is usually expressed as being obtained from by scaling by and then translation by so let me give a suggestion as to why this point of view might be a useful one to introduce.
The graph of consists of all those points such that . Similarly, the graph of consists of all those points such that . Let us start with a point . Then, by definition, . Now let us scale that point by and translate it by , both in the –direction. This results in the point . I claim that this is a point on . To show that, I need to convince you that . But this is immediate from the fact that .
I'd just like to note that there are other ways of looking at the connections between functions and graphs. Just as a line can be rewritten as so the equation can be rewritten as and we can think of it rather as looking at the zero set of a function . This can make the apparent disparity between and disappear since it treats them the same: instead of pre- and post-composing we simply pre-compose by suitable functions in both and . For example, if we pre-compose by an invertible affine transformation, say , then the zero set of is obtained by applying to the zero set of . This is the same argument as above, in that if is such that then if we set , we have:
and so is in the zero set of .
4.3 Adjoint Functors
One of the features of category theory is the plethora of adjoint functors. Sometimes it seems as though any functor worth studying is part of a pair of adjoint functors. Many, many years ago I asked on MathOverflow for an intuitive view of adjoint functors. I think that the best replies had a sense of partial inverse, or "nearest" solution to an unsolveable problem.
Perhaps surprisingly – or perhaps not if you have been keeping up so far – we can find adjoint functor pairs at a very early stage of school mathematics. Our category in this case is simply with an arrow if divides . There is just have one such arrow if it exists.
For purposes of illustration I need to pick a number and I'm going to use . There is nothing special about this number and everything I say would work equally well with any number (though and are a little bit special). This choice defines a subcategory of consisting of all multiples of which I will write as . We can now define some functors between these categories:
Let's start with the first of these, . This takes a multiple of and simply regards it as a number so "forgets" that it was a multiple of . There's clearly no inverse here as there's plenty of numbers in that aren't multiples of . So I want to find something that is as close to an inverse as I can find.
This means that given a number, which may or may not be a multiple of , then I want to construct a multiple of out of it. If I were to start with a number that happens to already be a multiple of then I want to stick with that number. Also, this has to preserve divisibility in that if divides then whatever goes to has to divide whatever goes to. Combining these two, we get that if happens to be a multiple of and divides then the result of applying this functor to must also still divide .
The solution is to send a number to its lowest common multiple with , which I've called in my list above. This has the required properties:
-
If divides then divides .
-
If is already a multiple of then .
-
If is a multiple of and divides then still divides .
The first of these is actually just saying that is a functor. It is the second two that establish that is adjoint to . (For those that know a bit about these, these two functors have a few extra special properties as well which is why the second statement is stronger than one might expect.)
Let's turn our attention to the other two functors. These are defined just on . We face the same problems trying to invert , multiplication by , as we did with : not everything is in its image. The naïve inverse is dividing by but that only works on things that are definitely multiples of . So we need something that will act as division by where that is possible but also still do something sensible when it isn't.
It turns out that the correct answer is to divide by the highest common factor of and (also known as the greatest common divisor). This is the functor above. What this does is to divide by as much of as it is possible to do.
The adjuntion rule means that for two numbers and then the following two statements are equivalent:
-
divides ,
-
divides .
5 So What?
I plan to expand on the "So What?" section of the original talk in another article, but it wouldn't be right to end this without a smidgen of "so what?".
Let me start with the "So definitely not". I am very definitely not suggesting that school students be taught category theory, nor even that teachers are. My point is much more simple than that. It is that if I can find category theory in school mathematics in an unforced way, then it is time to stop claiming that school mathematics is different to "real" mathematics. The analogy that I used in my talk was the following:
| School Mathematics | The Hobbit |
| University Mathematics | The Lord of the Rings |
| Research Mathematics | The Silmarillion |
You cannot find every theme from LOTR in the Hobbit, nor from the Silmarillion in LOTR. Even when they are there they are often simplified. But (to a large degree, particularly given that these are fictional stories2) the stories are consistent with each other. Themes are developed in the deeper works, expanded on, and explained, but not contradicted. In the Hobbit the animosity between Elves and Dwarves is largely taken as fact. In the LOTR it is developed further through the friendship of Legolas and Gimli. In the Simarillion it is explained through the history of the interactions of the races. But while each further work contains more than the Hobbit did, none tell us that what was in the Hobbit was actually incorrect.
2Apologies to anyone for whom that comes as a shock.
And that's what I would like to see between these branches of Mathematics.