1 Introduction

I recently had occasion to revisit my favourite proof of Pythagoras' theorem and discovered that it has depths that I had been unaware of. I learnt that it can also be used to prove other related results such as the parallelogram law. Slightly more surprisingly, there's a proof of the sine rule hidden in it and of a similar tangent rule.

2 Parallelogram Law

The parallelogram law states that in a parallelogram with side lengths $a$ and $b$ and diagonals $c$ and $d$ then these lengths are related by the equation:

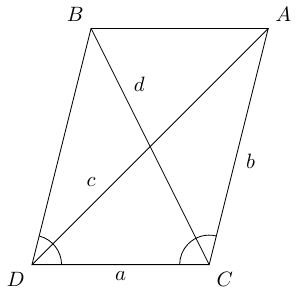
This can be deduced very simply from the cosine rule. Applying this to the two triangles $ADC$ and $BDC$ yields the identities:

The angles $C$ and $D$ add up to ${180}^{\circ }$ so $\cos (D)=-\cos (C)$ whereupon adding these two equations produces the parallelogram law.

It can also be proved using the core diagram of my favourite proof. The two triangles in the parallelogram both have two sides $a$ and $b$ so constructing the diagram for each leads to an isosceles trapezium with slant height $ab$. Placing these trapezia adjacent to each other leads to the following diagram.

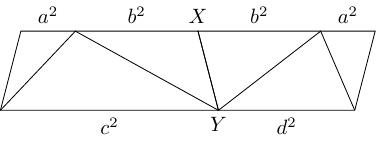
The key is that at the points marked $X$ and $Y$ then the angles on each side are $C$ and $D$ which add to ${180}^{\circ }$ so the top and bottom lines that appear straight genuinely are. Then the corner angles are all either $C$ or $D$ and so the shape is a parallelogram. Comparing the top and bottom lines gives the parallelogram identity. Thus the parallelogram identity is proved by constructing … a parallelogram.

3 Permutations

The original diagram has $c^2$ on the bottom and $a^2$ and $b^2$ along the top and so seems to put the focus on $c$ as a "special side". By placing a reflected second copy next to the first, this preference can be removed.

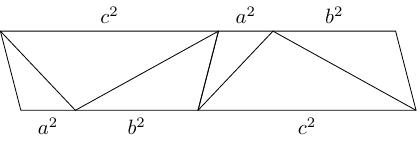
Taking any three sequential triangles proves the rule for one of $a^2$, $b^2$, or $c^2$. Also, the diagram can be wrapped around into a loop. Alternatively, a single diagram could be wrapped into a Möbius band. Cutting the band between any two triangles then gives the cosine rule for one of the edges.

4 The Sine Rule

By considering the height of the trapezium, we get the sine rule. The following diagram shows that this height is $ab\sin (C)$ (and if $C$ is obtuse then it also shows that we should define $\sin (C)=\sin ({180}^{\circ }-C)$).

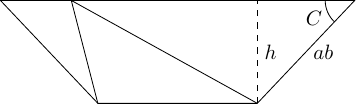
The permutation invariance shows that this height is the same regardless of which triangle is the central one. So the height is also equal to $bc\sin (A)$ and $ca\sin (B)$. This gives:

Dividing through by $abc$ gives the more usual form:

5 The Tangent Rule

The same diagram for the sine rule can be used to show a similar rule for the tangents of the angles.

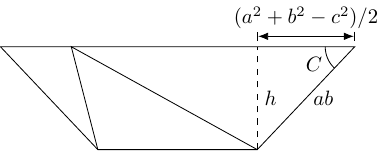
The overhang is $\frac{a^2+b^2-c^2}{2}$, so

Again, the invariance of the height under permutation (and multiplying by $2$) shows that:

The quantity $a^2+b^2-c^2$ can be thought of as a measure of how far the triangle is from being right-angled with $c$ as the hypotenuse, so $(a^2+b^2-c^2)\tan (C)$ is perhaps a normalised version of this that is independent of the side chosen for the hypotenuse.

(If this is new to you – it was to me – then it can also be deduced easily from the sine rule and cosine rule.)

6 Area of a Triangle

Let $A$ be the area of the original triangle. Then as the three triangles in the trapezium are scaled versions of that triangle, their areas scale with the squares of the length scale factors so are $a^{2}A$, $b^{2}A$, and $c^{2}A$.

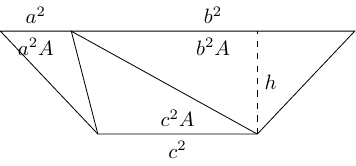
The total area of the trapezium is therefore:

Using the formula for the area of a trapezium, the area is also:

Equating these shows that the height of the trapezium and the area of the original triangle are related by $h=2A$. Combining this with the formula for the heights from the section on the sine rule gives the formula for the area as:

Also, from the tangent rule:

We can get yet another formula by applying Pythagoras' theorem (which we proved way back in the beginning of the original post) to the overhang triangle.

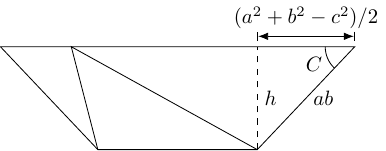
This yields:

Note that if the trapezium slopes the other way then we still get the same expression as the overhang distance is squared.

This simplifies as follows:

Picking up from the penultimate line, with a sign change to make life a bit easier,

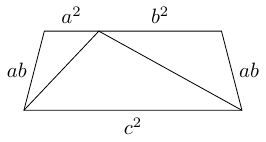
We have the expression $(a-b)(a+b)$ in the first part of this. This can also be found in the last part since:

(This is also an application of the parallelogram law with a degenerate parallelogram which has "sides" length $a$ and $b$ and "diagonals" $a+b$ and $a-b$.)

Substituting this in gives:

Substituting for the area, $A$, now gives:

And this is Heron's formula.

7 Which Trapezia?

In coding the diagrams for this article, at one stage I considered a strategy whereby I started with the trapezium and then constructed the triangles inside it. Although I eventually went for something else, that does raise the question of whether or not it is always possible to construct the triangle inside the trapezium. That is, starting with the outer trapezium in the following diagram then is it possible to construct the inner lines so that it works?

The lower edge determines the length $c$. The other edges determine the lengths $a$ and $b$. The simplest way to get $a$ and $b$ from those lengths uses the identities:

so by taking the sum of the three lengths, and the length of the top minus the lengths of the two slant sides then $a$ and $b$ can be found (the sign ambiguity when taking square roots translates into switching $a$ and $b$). However, this reveals a condition on the trapezium: since $(a-b{)}^2$ is equal to the top length minus both slant sides, that value needs to be positive.

So our first condition is that the top must be more than or equal to the sum of the two slant sides (if it is equal then $a=b$ so the triangle is isosceles).

Now given three lengths then we can construct a triangle from these lengths provided that the sum of any two is bigger than the third. So let us suppose that we have a suitable trapezium and have found the lengths $a$, $b$, and $c$ so that the top is $a^2+b^2$, the bottom is $c^2$, and the two slant sides are $ab$. Firstly, the combined distance up the left-slant, across the top, then down the right-slant must be more than the length of the bottom. So:

which, as everything is positive, square roots to $a+b>c$.

Secondly, the combined distance down the left-slant, across the bottom, then up the right-slant must be more than the length of the top. So:

This rearranges to:

which square-roots to $c>|a-b|$. This means that $c>a-b$ and $c>b-a$. From the first, $c+b>a$ and from the second $c+a>b$.

Hence the existence of the trapezium forces the necessary conditions for the triangle to be constructible, and so the only condition needed is that the sum of the lengths of the slant sides be less than or equal to the length of the top side.

8 Conclusion … for now

I've discovered quite a bit more about what my favourite proof of Pythagoras' theorem can do, to the extent that while I'm happy to conclude this here then I'm very hesitant to say that I'm done with it. I expect I will revisit it again and discover yet more lurking within. But for now I'm going to wrap this up and go make myself a Möbius strip with the diagram on it.