1 Introduction

The Area of an Annulus puzzle is something of a classic in geometry. Little surprise, therefore, that it forms the basis for some of Catriona Shearer's puzzles. Indeed, I think that the first one that I (loopspace) worked out a solution to involved areas of annuli.

An important skill in Mathematics is the ability to play with an idea. In this post, we want to show how playing with the classic Area of an Annulus puzzle leads Catriona to a puzzle and loopspace to a generalisation of the original construction.

2 Introducing the Puzzle, by Catriona Shearer

If I had to name a favourite puzzle, it would probably be the classic "area of an annulus". When I first saw it, it took me a while to believe that one measurement could possibly be enough information. Then, a few months ago, brilliant.org tweeted this animation which I really liked. It not only gives some sense of how the area changes as the line moves, but it was the first time I'd considered that the two circles didn't have to be concentric for the area to be the same.

When I write a puzzle, it tends to come about in one of two ways. Sometimes an idea will crop up and I try to hang onto it for long enough to write it down and explore whether it can become a puzzle. Other times, especially in the holidays, I start by sitting down with a bit of time and a blank sheet of paper. The problem then is getting started – what to draw first – so I often start by sketching out problems I've seen in the past which I particularly like, and then playing around with them to see what else is interesting about the diagram, or if I can use the same idea in another situation. Starting with the brilliant.org picture, I realised that the area would be the same as the semicircle balanced on the line, which meant that removing the same area from both would still leave them equal.

3 Extending the Idea, by loopspace

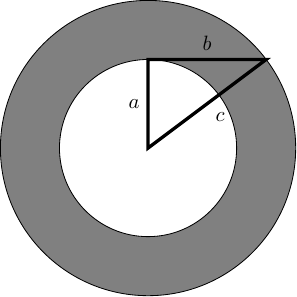
As Catriona says above, this puzzle is "all about" the classic area of an annulus problem. The classic proof of this result, namely that the area of the annulus in Figure 2 is $\pi b^2$, involves drawing a right-angled triangle relating the various involved lengths, as in Figure 2.

The proof goes as follows. The area of the annulus is the difference of the areas, which is $\pi c^2-\pi a^2$. The triangle is right-angled (as the line length $b$ is tangential to the inner circle), meaning that $c^2=a^2+b^2$. Putting these two together yields:

$$\pi c^2-\pi a^2=\pi (c^2-a^2)=\pi b^2$$

and so knowing $b$ is sufficient for calculating the area.

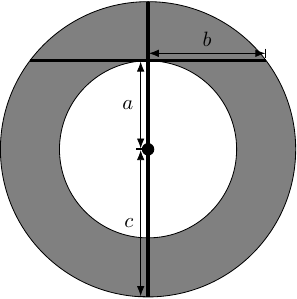
I want to do two things with this idea. The first is to rewrite the formula for the area as follows:

$$\pi c^2-\pi a^2=\frac{1}{2}(2\pi c+2\pi a)(c-a)$$

In this formula, $c-a$ is the "width" of the annulus, while $\frac{1}{2}(2\pi c+2\pi a)$ is the average of the circumferences. This is reminiscent of the formula for the area of a trapezium.

There's a nice way to make this not a coincidence. But that's not the main thing I want to look at here.

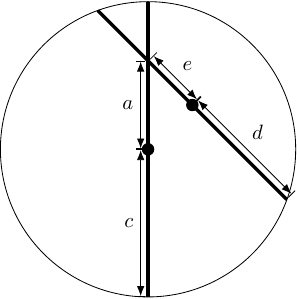
I've been thinking about Pythagoras a lot. One of the things I've discovered is that Pythagoras' theorem is equivalent to the Intersecting Chords theorem in a very direct manner. The diagram proving Pythagoras from Intersecting Chords is very similar to Figure 2. It looks like Figure 3.

The Intersecting Chords theorem says that:

$$(c+a)(c-a)=b^2$$

which rearranges to give Pythagoras' theorem, but which also directly proves that the area of the annulus is $\pi b^2$ without invoking Pythagoras' theorem.

At this point, the use of Intersecting Chords instead of Pythagoras feels a bit like semantics: you say "Pythagoras", I say "Intersecting Chords". The advantage of bringing in Intersecting Chords is that it separates the idea from the necessity of a right-angle: in the Intersecting Chords theorem there is no requirement that the chords intersect at right-angles. Figure 4 shows an alternative configuration, but note the slightly unusual choice of which lengths to label.

The marked point is the midpoint of that chord, so the length $d$ is half of the length of that chord.

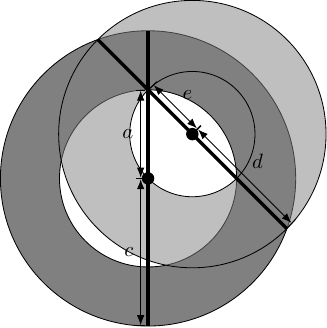
Applying the Intersecting Chords theorem yields:

$$\begin{array}{rl}(c+a)(c-a)& =(d+e)(d-e)\\ c^2-a^2& =d^2-e^2\\ \pi c^2-\pi a^2& =\pi d^2-\pi e^2\end{array}$$

The left-hand side is the area of the original annulus. The right-hand side is the area of an annulus based on the second chord: with outer circle of radius $d$ and inner circle of radius $e$.

This means that as the second chord rotates (keeping the intersection point fixed) it generates a family of annuli which all have the same area. At one extreme, we get the original annulus. At the other, we get the circle.

There's plenty to explore with this, but I'll end with a generalisation of Catriona's puzzle: in Figure 6 the cyan region has area $4$; what is the combined area of the magenta regions?