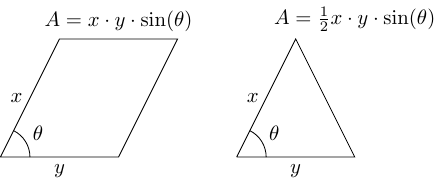Contents
Last night I dreamt I proved Pythagoras' Theorem again1.
1I originally thought of going with "It is a truth universally acknowledged, that a mathematician in possession of a proof must be in want of a theorem." but I've already used that one.
1 Introduction
The purpose of this article is to explore the following question.
How should we geometrically view multiplication?
The two choices I want to focus on are area and similarity. That is, when thinking about the product , should we picture a rectangle with sides and , or a length which is in proportion to as is to ?
I will be upfront about my own preference: it is for similarity. However, to justify that preference I feel I have to play Devil's Advocate and explore the area picture. Obviously, to represent we can simply draw an appropriate rectangle. The usefulness – or not – of the picture comes when we try to manipulate it. The first stage of such manipulations is often to have two equal products, which leads to the following:
Given two rectangles, known to be of the same area, how can this equality be demonstrated geometrically?
I have been accompanied on my exploration by two standard results in Euclidean geometry: Pythagoras' Theorem and the Intersecting Chords Theorem. Pythagoras' Theorem is often proved in school using a decomposition of areas, but I don't like that proof. The statement of the Intersecting Chords Theorem says that two multiplications of lengths produce the same answer, but the lengths being multiplied lie in the same direction and so there is no obvious area involved. My goal, therefore, was to produce area-based proofs of Pythagoras' Theorem and of the Intersecting Chords Theorem that don't make me cringe.
1.1 Acknowledgements
This article has been brewing for quite some time. I can trace it all the way back to a neat proof of the double angle formula which I tried to extend to the compound angle formula. It has also been heavily influenced by the puzzles of Catriona Shearer on Twitter (also collected into a book) which have made me look afresh at area. It has benefited from numerous discussions both on Twitter and with my colleagues.
2 Setting the Stage
It is useful to consider transformations when working with area, There are several standard types of transformation and they have differing properties with regard to shape and area.
Rotations, reflections, and translations all preserve both shape and area. Uniform scaling preserves shape but not area. Non-uniform scaling doesn't necessarily preserve either shape or area. Lastly, there is the shear which preserves area but not shape. As we want to do something that changes shape but not area, shearing therefore seems to be the most promising starting point.
Our strategy throughout this article will be to find a diagram that uses a shear to demonstrate that two shapes have the same area. To find the diagram we will inevitably use the fact that the two shapes have the same area but once we have the idea of the diagram we will then use it to try to prove our two test cases: Pythagoras and the Intersecting Chords Theorem.
The flow of the reasoning is important to recognise here. In finding our diagrams we will often be assuming the result that we're wanting to show. But once we have the shape of it, we will forget where it came from so that we can use it to prove one or other of the theorems.
In the remainder of this section we shall introduce the main players in this article: Pythagoras' Theorem, the Intersecting Chords Theorem, and shears.
2.1 Setting up Pythagoras
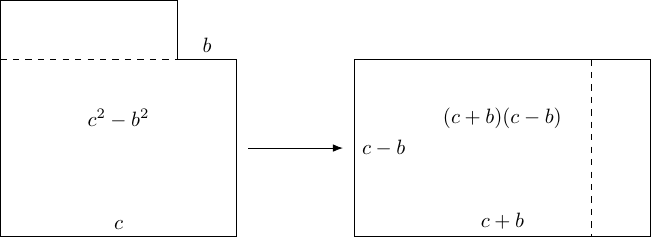
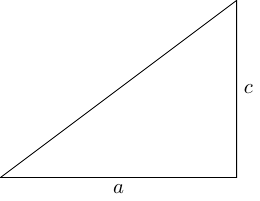
Pythagoras' Theorem doesn't traditionally involve showing that two multiplications are the same. We therefore need to manipulate its usual statement slightly to a more appropriate form. Algebraically, we shall rewrite as:
Geometrically, we can represent the right-hand equality as in Figure 1.
2.2 The Intersecting Chords Theorem
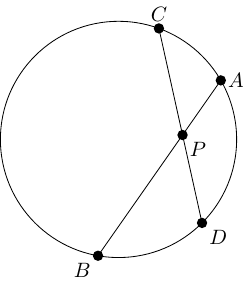
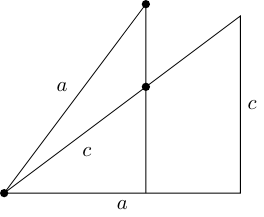
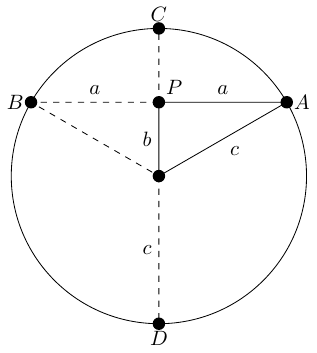
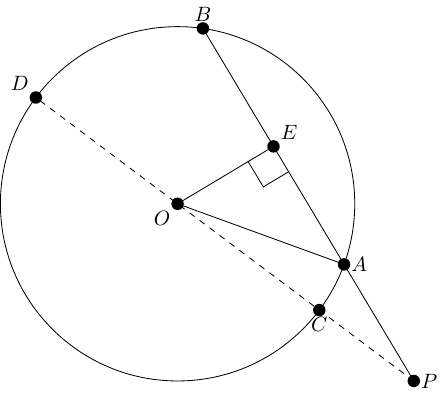
The Intersecting Chords Theorem states that in Figure 2, then the following equation holds.
|
The standard way to prove this is to use similar triangles. Thus the result should be written as:
|
The difference ought to be negligible, but perhaps because my brain was preoccupied with areas, Equation (1) felt as though it really ought to be about areas. So Equation (1) feels as though it ought to be saying that two shapes have the same area.
2.3 Rectangles and Parallelograms
While best represents the area of a rectangle, we'll also want to work with more general shapes such as triangles and parallelograms. Our and will be neighbouring sides of these shapes, and the key observation is that if we vary and but keep the angle between them fixed then the area of the shape is proportional to with fixed constant of proportionality.
While we'll start with rectangles, we'll soon move on to parallelograms and triangles.
2.4 Enter the Shear
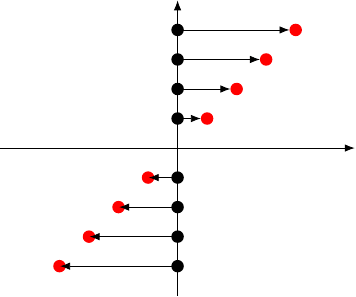
A standard shear parallel to the –axis moves every point horizontally a certain distance depending on its distance from the –axis and a shear factor, as in Figure 4.
That a shear preserves area follows from the formula for the area of a parallelogram: under a shear, a rectangle is deformed to a parallelogram with the same base and perpendicular height and so the same area.
This, however, is a small snag with shears: they have a tendency to transform rectangles into parallelograms and we want to transform one rectangle into another. Fortunately, it can be shown2, that any (non-trivial) shear has a unique pair of lines which start out at right-angles to each other and end also at right-angles to each other. Moreover, each line is stretched by a different factor. Knowing that this exists, it isn't hard to reverse engineer the process to start with the two rectangles and end up with the requisite shear.
2Using the Singular Value Decomposition.
3 Shearing Rectangles
In this section we shall consider how to shear one rectangle into another. As mentioned earlier, there is a result from the theory of linear transformations (the Singular Value Decomposition) which implies that for any linear transformation it is possible to find rectangles at very specific angles to the axes such that one is transformed to the other. Since shears preserve area, when applied to a shear then this construction ensures that the rectangles will have the same area.
Although we can use the Singular Value Decomposition to find the necessary angles, once we know that they exist it turns out not to be too hard to find them.
To figure out the construction, we start with two rectangles of the same area. We can express this algebraically by letting the first rectangle have sides lengths and , and the second and . That they have the same area means that:
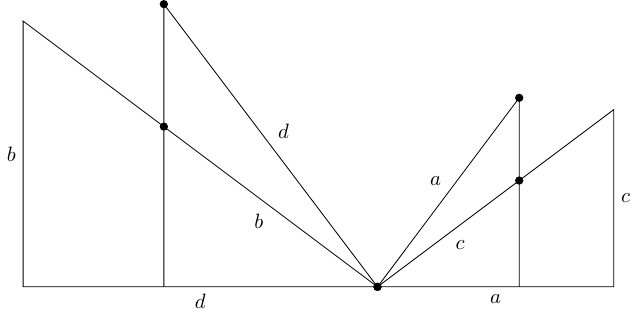
Let's start by noting that we may as well assume that the numbers are all strictly positive and not all the same. We can further assume that for ease of drawing. We make a diagram as follows.
-
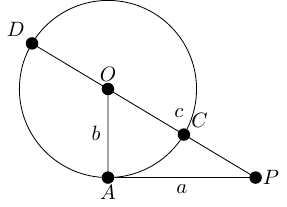
Start with a right-angled triangle with base along the horizontal and height vertically. The vertex opposite should be at the origin. See Figure 5.
-
Now mark the point on the hypotenuse of distance from the origin. From here, drop the perpendicular to the base and extend it upwards to a point that is distance from the origin (here's where we use the assumption that to say that this point is higher), as in Figure 6.
-
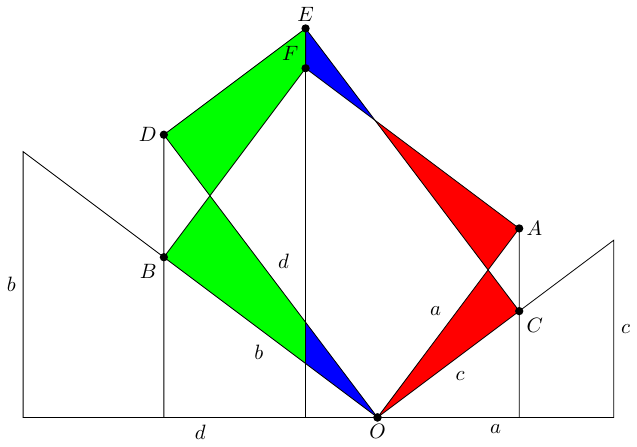
Now do the same the other side with the lengths and . Since , we have . This results in Figure 7
-
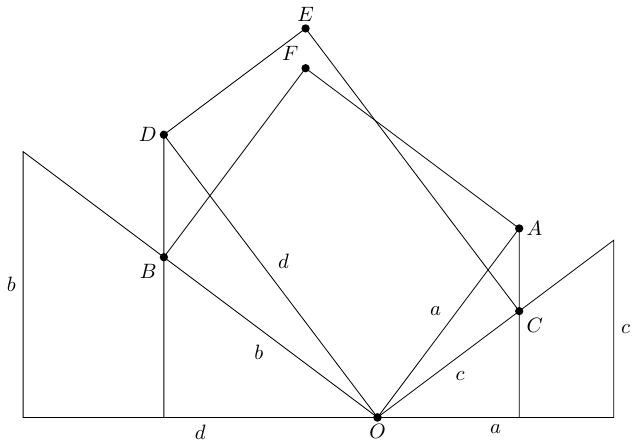
The four triangles are all similar, albeit with rotations. To show that the triangles on one side are similar to the ones on the other uses the assumed property of the numbers: that . The similarities implies that we can produce rectangles with sides and as in Figure 8.
At this point, we have a choice as to how to proceed. If we are happy with shearing, we can apply a vertical shear to rectangle . The shear to apply brings down to . On the other side of the vertical line through , point will go up. The way that shears work is controlled by similar triangles, meaning that will rise up to meet . That is, the shear will take rectangle to .
The alternative method uses the overlap to determine a decomposition, as in Figure 9.
3.1 Shear Pythagoras
With a small adjustment to the angle, this can be used to prove Pythagoras' Theorem. Recall that we're aiming to show that:
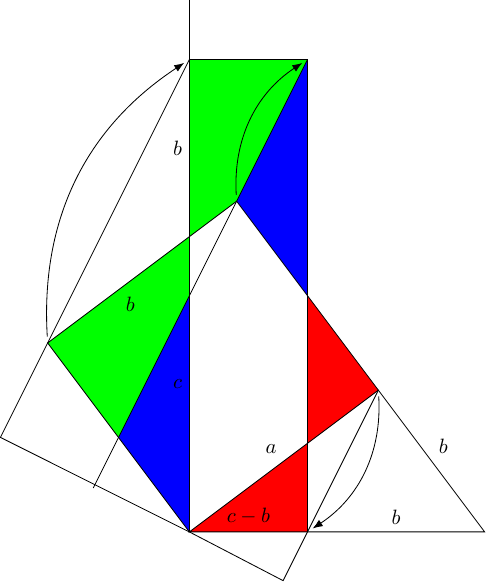
Thus our goal is to show that the rectangle with sides has the same area as a square with side . We shall use essentially the same method as before, but rotated slightly. We start by placing the –– triangle on the –axis with the hypotenuse horizontal and the vertex opposite at the origin. This means that the side length points from the origin into the first quadrant. The final diagram is in Figure 10.
In this diagram, we can either apply the shear which moves points according to the arrows, or we can do the indicated dissection. Either way, we deduce that and hence that Pythagoras' Theorem is true3.
3I couldn't find this proof, either by shearing or by dissection, in the list on Cut The Knot so would love to know who first came up with it.
3.2 Shear Chords
The difficulty with applying this to the Intersecting Chords Theorem is two-fold. The first issue is that it does nothing to address the fact that each pair of lengths that are multiplied in the Intersecting Chords Theorem lie in the same direction, so there's no obvious shapes to construct. The second issue is that our construction is for rectangles, and there's no requirement in the Intersecting Chords Theorem that the two chords be at right angles.
4 Different Angles
To address the difficulties in applying the above to the Intersecting Chords Theorem we need something a little more flexible. Unsurprisingly, it was another of Catriona Shearer's puzzles that set me off on the track to find it. The key is to offset the origin from its "obvious" location in the diagram. To see how this works, we need yet another shape: a trapezium.
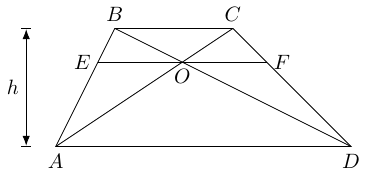
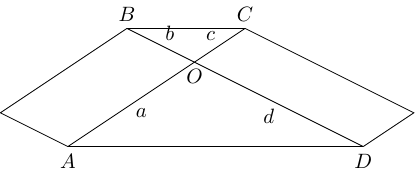
Consider a trapezium, and draw in the diagonals, as in Figure 11. We also draw in the horizontal at the point where the diagonals cross.
There are lots of interesting facts about this trapezium. First is the fact that the triangles and are similar (with corresponding to and to ). This in turn means that triangles and have the same area, since and the angles at are the same.
The length is the harmonic mean of the lengths and , which is given by the formula:
Moreover, bisects so that .
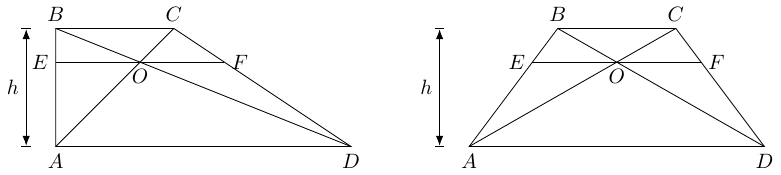
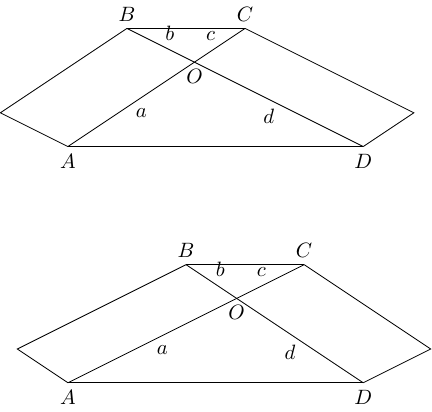
All of these can be shown directly, but they can also be shown with a little shearing. Applying a horizontal shear to this trapezium will change it in some respects but not in others. Crucially, a horizontal shear doesn't change area or horizontal distances. We therefore apply two shears, one of which makes vertical and the other which makes it into an isosceles trapezium. These are shown in Figure 12.
Having sheared to make vertical, we can see that the area of triangle is . From the shear to make it isosceles, we deduce that triangles and are of equal area since when the trapezium is isosceles case then they are congruent. By a similar reasoning, .
For our purposes, the main thing to spot is that this shearing has changed the shapes of triangles and without changing their areas. By reverse engineering this construction, we can get another geometric demonstration of when two rectangles have the same area.
4.1 Trapezium Shearing
We'll generalise slightly here. Rather than considering two rectangles with equal area, we will consider two equi-angular parallelograms with equal area. As before, the starting equation is to have four numbers satisfying:
but we will assume that these are sides of two parallelograms which have the same angles.
As they have the same angles, we place them touching each other at a vertex so that their adjoining sides line up, as in Figure 13.
The fact that these parallelograms have equal areas means that the triangles and are similar, whence the lines and are parallel. This means that shearing parallel to moves across. In particular, if we shear it so that the image of is the mirror image of then the two parallelograms will have been sheared into each other, as in Figure 14.
4.2 Shear Pythagoras, Again
The trapezium method can also be used to prove Pythagoras' Theorem. The most natural construction is why I introduced parallelograms. Figure 15 shows the construction.
The Alternate Segment Theorem says that the two marked angles are equal, and this is sufficient to show that is parallel to and hence that the trapezium argument can be used to show that .
It is, of course, possible to trace the angles further round to see that the triangles and are similar, whence
from which Pythagoras' Theorem follows.
Again.
4.3 Shearing Chords
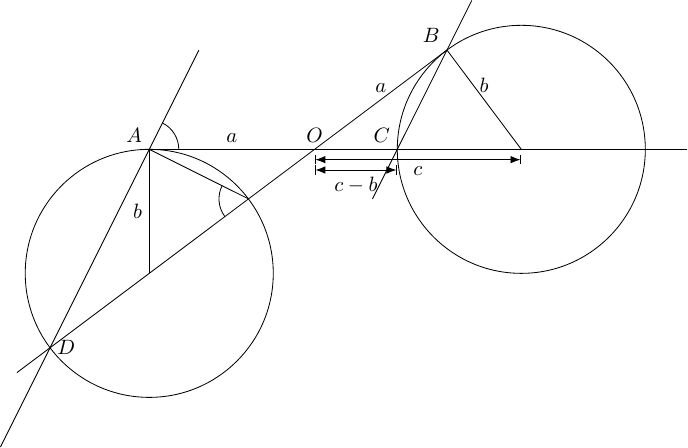
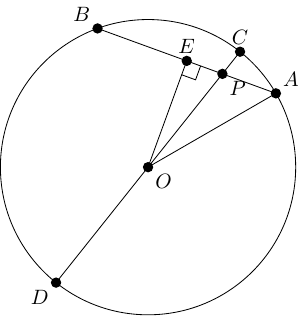
As mentioned earlier, the issue with using area to prove the Intersecting Chords Theorem is that the lengths that are multiplied lie in the same direction meaning that it is difficult to make a two dimensional shape out of them. We therefore have to do something which breaks that. The answer turns out to be to include a reflection. The resulting diagram is in Figure 16.
In this diagram, the reflection line bisects the angle . Points and are reflected to points and . The so-called "Butterfly Theorem" (aka "angles in the same segment are equal") shows that the lines and are parallel, whence is a trapezium.
The Trapezium Shear then says that the two side triangles in this trapezium have equal areas, whence the triangles and are of equal area. The area of is a multiple of and that of is the same multiple of . Hence:
as required.
Similar arguments work for the cases where the intersection point is outside the circle and where one of the chords is tangent to the circle.
5 Conclusion
I have what I sought: area proofs of Pythagoras and the Intersecting Chords Theorem that don't make me cringe. However, neither do they convince me that area is the right concept here. In particular, the lengths (ha ha) I had to go through to get the proof of the Intersecting Chords Theorem only serve to underline how natural is the original proof by similar triangles. I do feel, though, that I gave it a good try and can now feel more secure in my assertion that these results are truly about similarity and not about area.
If you, dear reader, are less convinced, I can leave you with a few things to ponder.
First is an attempt to answer the question as to why Pythagoras' Theorem is so tied in the collective consciousness with area. This, I think, is due to the fact that there are very few "small" numbers and sometimes two things are associated with the same number without the concepts themselves being associated. If I can get technical for a moment, Pythagoras' Theorem concerns the –norm in . There are two s here. The first, in "–norm", relates to the fact that the terms in Pythagoras' Theorem are squared. The second, in "", actually relates to the fact that there are two terms on one side of the equation but also brings in area as the measure of shapes in . The crucial observation is that these two s are not related. We can vary each of them without affecting the other and get similar statements to Pythagoras' Theorem. For example, the diagonal of a cuboid in is given by a Pythagorean formula involving its three side lengths. One would, I hope, hesitate before introducing squares to demonstrate this directly4.
4Taking this to the extreme leads to the somewhat absurd attempt to justify the formula for standard deviation as minimising the areas of actual squares.
Second is a question as to which of area and angle is the more fundamental concept. If you know any measure theory, you'll know that defining the concept of area correctly is quite subtle and there are many counter-intuitive aspects such as null sets and non-measureable sets. Angles, on the other hand, are far more straightforward. Here's a thought experiment to demonstrate this: it is simple to define a rectangle in terms of lengths and angles; now imagine you knew how to determine length and area – could you still define a rectangle? To make life a little easier, I'll allow you the notion of parallel lines.
6 Epilogue
While traversing this journey, I have had time to explore quite a few offshoots which haven't made it into the main storyline. There are some of them which I would feel a sense of loss if I didn't record them somewhere nearby, so in no particular order here are the ones that I have most affection for.
6.1 Harry Potter's Scar
I first actually started thinking about the ideas that would eventually condense into this article after a visit to Harry Potter World. Figure 17 is a picture of Harry Potter's Scar.
As we now know, the two parts of the scar have equal area.
6.2 Equivalence of Pythagoras' Theorem and the Intersecting Chords Theorem
The two results I've been working with throughout this investigation are Pythagoras' Theorem and the Intersecting Chords Theorem. Both are equivalent to the statement "Similar triangles are similar", which is itself equivalent to Euclid's fifth postulate. So it is no surprise that they are equivalent to each other. Nevertheless, it is quite nice to find direct proofs of their equivalence.
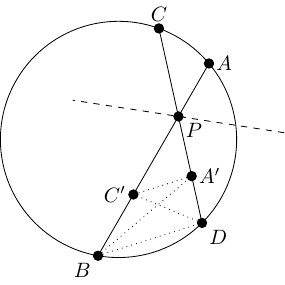
First, from the Intersecting Chords Theorem to Pythagoras' Theorem. We give two proofs of this. Both actually prove .
In Figure 19, the Intersecting Chords Theorem says that:
whence Pythagoras.
The second version, Figure 19, uses the tangent form of the Intersecting Chords Theorem.
In this version, the Intersecting Chords Theorem states that:
The other direction is slightly more complicated because there aren't obvious right angles in an arbitrary Intersecting Chords diagram. The strategy to take, therefore, is not to use an arbitrary diagram but a special case which can then be used to deduce the full version. We'll start with the case where the intersection point is inside the circle.
In Figure 20, triangles and are right-angled. Hence:
Whence:
as required.
Since and are arbitrary, this holds for any chord passing through and hence the general case follows.
In the second case, where the intersection point is outside the circle, again we examine a special case with the diagram in Figure 21.
As before, and are right-angled triangles. Almost as before, Pythagoras' Theorem leads to:
The same argument then results in:
and the general case follows from this by the same reasoning as above.
For the tangential version of the Intersecting Chords Theorem we run the argument from Figure 19 backwards. Pythagoras shows that in Figure 19 we have , and then from the above we can extend that to any extended chord through .
6.3 Actually Proving Pythagoras
This last epilogue relates to the question "What does it mean to actually prove something?". This isn't the place to expand fully on this, but I do have a couple of things to say in regard to this question with regard to Pythagoras' Theorem. Although I've written about many proofs of Pythagoras' Theorem, both here and elsewhere, nowhere have I considered the question as to which proof I would use if I wanted to convince myself of its truth.
That is to say, suppose I suddenly woke up one morning and doubted the truth of Pythagoras' Theorem. How could I convince myself that it was true?
This isn't about demonstrating it to a student, or figuring out the deep meaning behind it, but just verifying that it is true. Here's what I'd use:
Let be an inner product space with inner product and associated norm . Then for such that we have:
The problem with that is that it doesn't have much to do with what one might call a real triangle. It is the abstraction of what it means for Pythagoras' Theorem to be true. So the more usual Pythagoras' Theorem could be restated as saying that this idealised situation models the real world.
On the scale perceptible to humans, space is accurately modelled by an inner product space.
The "proof" that I'd consider for this might read a little strangely. The part to focus on is the leap from the "real world" to the mathematical abstraction. We have to find a property of the real world that forces us to live in the type of world where Pythagoras' Theorem is true. The simplest that I've been able to pull it back to is the fact that the world looks the same from all directions, the so-called Gallilean principle of relativity. The proof then reads something like the following.
Wherever I stand, when I turn around then I don't perceive any difference in how the world looks. Therefore, rotation is an isometry and so the (local) isometry group (of a two-dimensional space) has a one-parameter compact subgroup. A one-parameter compact subgroup is conjugate to the standard orthogonal group, and therefore the metric is (locally) derived from an inner product. Hence Pythagoras' Theorem is true on the level that I can perceive.
Ultimately, these two encapsulate Pythagoras' Theorem for me: on the one hand there is the abstraction wherein it is almost obvious and on the other there is the question as to how well Mathematics models the real world.