Contents
1 Introduction
Here's the problem of the Birthday Parallelogram:
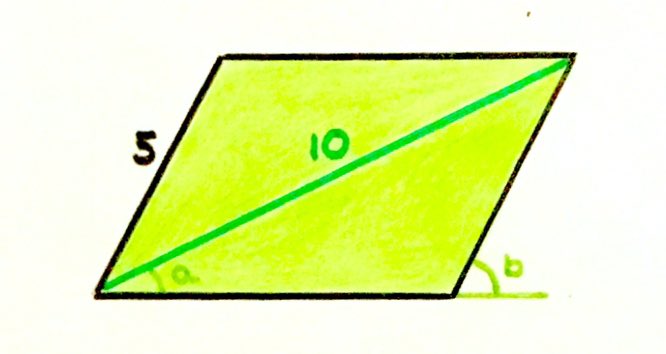 is a right angle. What's the area of the parallelogram?
is a right angle. What's the area of the parallelogram?
I (loopspace) picked this problem for the next in our occasional series for a couple of reasons. One was to do with my approach to solving it: I had a very definite idea early on as to how to solve it which took me some work to implement. So I knew I'd have something to write about in my part of a post on this problem. I also felt that despite having solved it, I had no concept of where it had come from. Usually, a solution will reveal the structure of the problem but in this case I felt that I had no feel for where it had come from.
Catriona's initial response was:
Funny you should ask that – there is a story, and to be honest I'm not a massive fan of that puzzle because I thought it was a bit contrived. But it was my birthday on Tuesday, so I was particularly keen to make a certain answer!
which showed that my instinct for a Mathematical story was working well! When she sent me her explanation of where it came from, she commented:
I feel this story is going to be something of a let-down now, but here it is!
It was anything but!
What I particularly love about the story is that Catriona had a definite goal in mind for the answer and this has coloured her view of it. I guess that most of her puzzles are explorations and a puzzle emerges organically so she doesn't set a puzzle unless she's happy with it. Here, because she had a target in mind she feels more constrained and so less content.
This reflects, I think, two modes of doing Mathematics. There is exploratory Mathematics, where one is simply exploring ideas. Here, one is open to serendipity and the treasures that one finds are evaluated purely on their own merits. Then there is directed Mathematics, where one has a destination in mind. In this situation, any potential treasures tend to be evaluated in the context of whether they help make progress towards that goal.
Both are necessary. I recently heard of a quote from George Hart in which he said:
The more Mathematics you know, the more you can make.
The exploratory mode helps you build your knowledge so that when you have a destination in mind, you have built strategies to get you there.
But that's enough from me for the moment, I'll hand over to Catriona for the story behind the puzzle.
2 The Birth of the Birthday Parallelogram Puzzle, by Catriona
This puzzle was an unusual one for me. Most of my puzzles come about as the result of several pages of scribbles – I have a notebook full of sketches and half-hearted attmepts at algebra squeezed in the space around a few neatly drawn puzzles. Usually a few hours of this kind of doodling will uncover a relationship that I can build a puzzle around, and if anyone else is in the room at this point I'll ask them to name a favourite number which becomes the given side length, or area, or angle.
For this puzzle, though, I started with the answer and tried to build a puzzle around it. About a week before my birthday, I decided it would be fun (yes, really) to post a puzzle on the day itself where the answer was my age. I briefly tried to write a puzzle like this last year, and failed to come up with anything, but this year's age seemed like a much easier target.
It turned out to be much harder than I thought. In fact, I was really struggling to come up with any ideas for puzzles at all, let alone one I could manipulate into having the right answer.
I can credit Ben Orlin for the inspiration that came next: he asked me to name a few puzzles from December that he could put together into a blog post. Flicking back through, I had fond memories of this one:
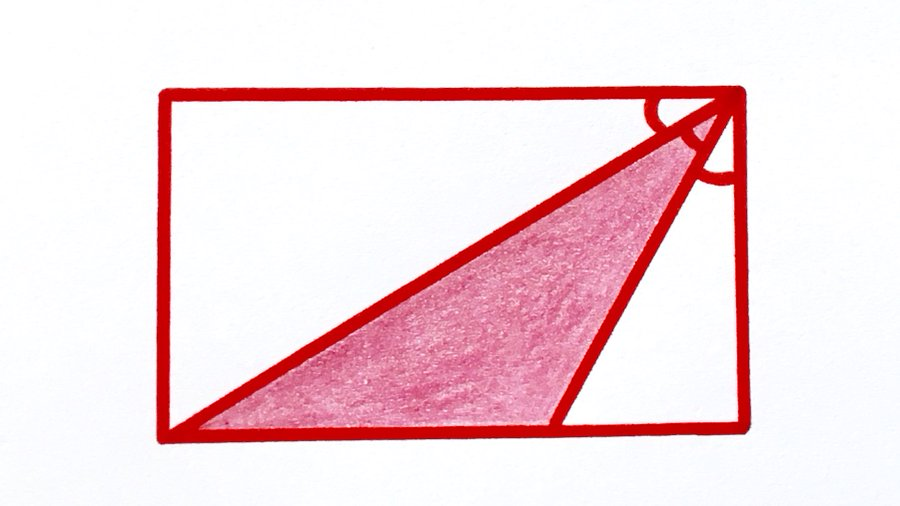
I particularly liked the fact that the two white triangles in the diagram above are similar, because we're told their smallest angles are equal. What if these two angles stayed equal, but the angle inside the red triangle changed? This would change the aspect ratio of the rectangle and so give a different shaded fraction – hopefully I would be able to choose numbers that would give me the answer I wanted.
[Warning: The next bit contains partial spoilers for both the parallelogram puzzle and the puzzle above]
The original equal-angles puzzle had split the base of the rectangle in the ratio , so I decided to start by altering this ratio.
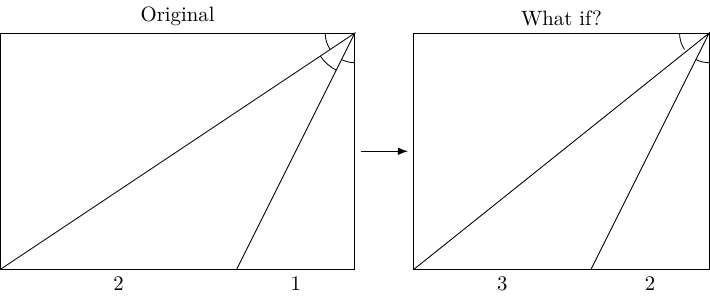
My first attempt was splitting it in the ratio , but this produced fairly horrible numbers for the other side lengths – no good, since I wanted an integer answer out of all this! However, my second attempt (a ratio of ) was much more promising – the height was now an integer.
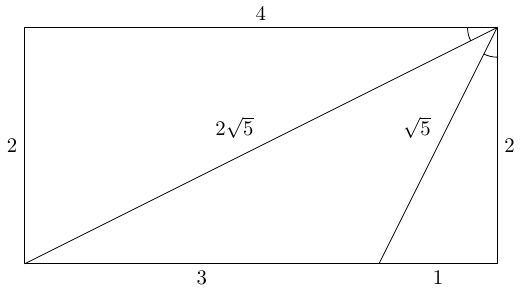
I used Pythagoras' theorem to work out that the two sloping lines had lengths and . Given that I'd started with similar triangles, it was no surprise to see one length was double the other – but the appearance of was a good omen for my target answer. Scaling these lengths up by would make them both integers and scale up any areas by a factor of . In fact, it made the area of the central triangle exactly half the target I was aiming for.
I was pretty pleased with this puzzle, and probably would have published straight away if I wasn't still harbouring hopes of making a particular answer. How hard could it be to change the puzzle so that the answer doubled?
Scaling up, my usual trick, was out. In the puzzle I'd specified two lengths ( and ), but the answer was an area. To double the answer, I'd need to have lengths and , which spoiled the simplicity I was aiming for.
Another option would be to keep the same lengths but somehow double the area to create either a parallelogram or an arrowhead. I sketched out both, and decided to go with parallelogram.
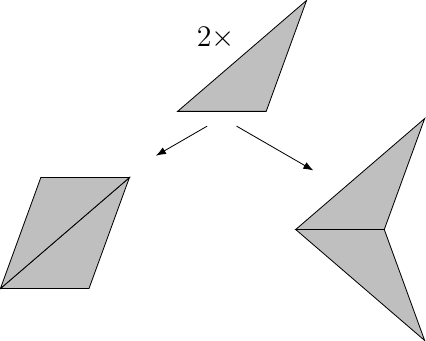
The next problem was how to show the two equal angles, since enclosing the parallelogram in a rectangle looked a bit odd. Eventually I settled on marking out both angles from the horizontal along with the condition that together they made a right angle.
To be honest, I still wasn't completely happy with this puzzle – I still couldn't get over the idea that I'd just spoiled a nicer puzzle by trying to contrive a different answer. The fact that the question needs an extra condition about the marked angles also feels less neat than I'd like. It's been interesting that I've had quite a positive response to it, both on twitter and from other people I've showed it to – which has reminded me that I'm not always a great judge of what other people think is a good puzzle.
3 Solving the Puzzle: the Hunt for the Right Angle, by loopspace
In the discussion of the solution, I will present three solutions. Catriona had a technique in mind, and I'll start with that. Then I'll present my original solution. After commenting on the solutions others have posted, I'll present an alternative which, I think, is different in approach to those others.
3.1 Catriona's Solution
Catriona included the following for this section:
I've given this puzzle to a couple of my colleagues, one of whom then gave it to his students (which I walked in on!). They've generally found it pretty hard, especially the students. The hints I've been giving are:
Enclose the parallelogram in a rectangle and write on everything you know.
Look for similar triangles.
I feel like my thinking is very heavily influenced by the idea that the parallelogram should really be sitting inside a rectangle, but that wouldn't necessarily be an obvious first step – I just can't not see it since I constructed the puzzle that way.
So let's take her advice and enclose the parallelogram in a rectangle. Writing on everything we know involves the angles. Since , whenever we have a right-angled triangle with one of or in it then the other angle in the triangle is the other of or .
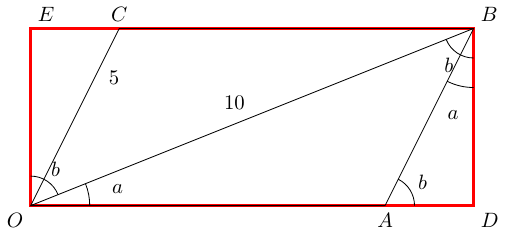
We're now exhorted to look for similar triangles. The angles say that the right-angled triangles and are similar. The hypotenuses of these are and respectively, so the scale factor is . This says that is half of , and is half of . If we put , so , then Pythagoras tells us that , so . Then and so the area of the parallelogram is:
3.2 My Approach
In solving this puzzle, I fixated on two parts of the information given. Firstly, we were given that , so I wanted to see a right-angle built from an angle and an angle . Secondly, we were given the lengths and , so I wanted to get them in such a position where they could be easily used to calculate an area, meaning finding lines of those lengths at right-angles to each other.
Therefore, I went hunting right-angles which were obviously of the form . My first attempt was:
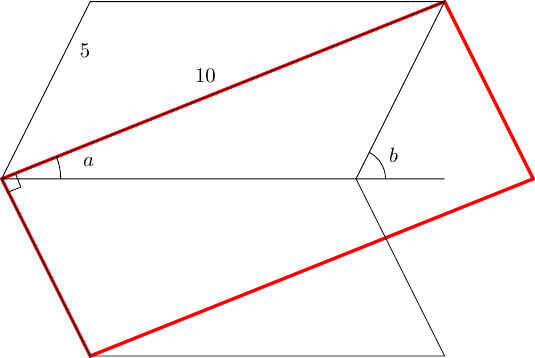
But I couldn't get this to work. So the next diagram I drew was the following.
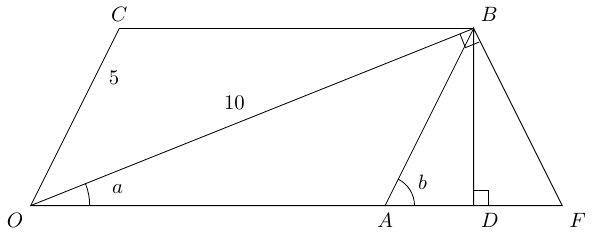
In this picture, is on the line from through and is such that the angle is a right-angle. Then is directly below on this same baseline.
This picture proved more promising. The triangle is right-angled, with angle at , so the angle at is . This makes triangles and congruent, meaning that has length . The triangle therefore has base and height so has area .
Then triangles and are similar with scale factor . So triangle has area times that of , which means that has area one fifth of , namely . As triangle is congruent to , this also has area . Thus triangle has area .
Finally, parallelogram has area twice this, whence .
3.3 Other's Solutions
Looking through the various solutions (see the replies to Catriona's tweet), I would say that they all take the line that the relationship implies that there should be a right-angle somewhere in the picture, either as a right-angled triangle with angles and , or as a right-angle split into .
Following that, similar triangles – sometimes in the guise of trigonometry – seems to be the natural next step.
So I think I'd relax Catriona's first hint slightly to:
What right-angles can you add to the diagram?
After that, if they needed another one then I'd offer the one about similar triangles.
3.4 An Alternative Approach
Memory can play tricks. I was convinced that someone had posted a solution to this puzzle that had surprised me with its simplicity. I can't find it now in the comments, so I suspect I was thinking of a different puzzle. While in the fuzzy state of being convinced that it existed but not having found it, I tried to recreate it. It isn't jaw-droppingly simple, but I think it does present a different view.
I was intrigued by the fact that the rectangle with sides and had area while the parallelogram had area . This meant that rectangles should fill the same area as parallelograms. After experimenting considerably with polygons in Geogebra, I ended up with the following diagram.
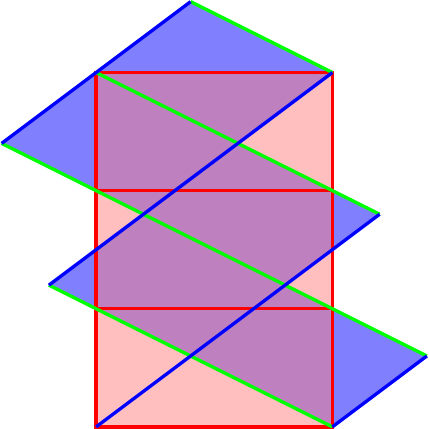
To demonstrate that this diagram really does show that five parallelograms is the same as three rectangles, we need to show that the intersections that appear to be half way down each side genuinely are half way down each side.
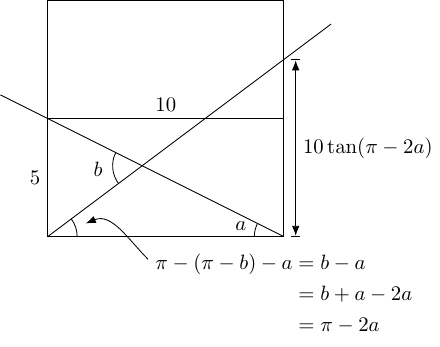
So we need to compute , knowing that . We can do this using the double angle formula for tangents (if you feel that this is cheating, this contains a diagram demonstrating it using similar triangles):
Then:
Hence the intersection point is at height , which is halfway up in the original diagram.
Thus the areas that appear to match up really do and thus five parallelograms has the same area as three rectangles, so the area of a single parallelogram is:
4 Conclusion, by loopspace
I'm not a fan of puzzles that rely on a secret (such as Langley's Find the Angle puzzle). Catriona's puzzles usually fall far of that and one thing I enjoy is seeing all the different approaches that people take in solving them. Without putting words into her mouth, I suspect that one reason why Catriona felt uneasy about this puzzle was because she was worried that it seemed to rely on spotting a "secret" (the surrounding rectangle). In truth, it relied on finding a right angle and didn't seem to depend on one particular one, so in the end it didn't require one to spot exactly what the puzzle setter had in mind. Nonetheless, the solutions did all seem to take a much more similar route to each other than I've seen in other puzzles. Of course, it's possible that unconsciously Catriona steered people towards it in the way it was set.
But yet again, a puzzle has turned out to be far more than just a puzzle and we hope that by showing some of the detail behind where it came from and how one might solve it, we've shown that Mathematics doesn't exist in isolation but each idea has a story behind it.
