1 Introduction
When is a circle a circle?
It is quite common in Mathematics to have several descriptions of something. Understanding why the different descriptions are of the same thing can be very illuminating. A very simple example would be that or that .
I recently came across a description of a circle that I hadn't encountered before. It was given in terms of complex numbers, though it doesn't need them. Pick two points on the plane, and fix a ratio1, then take all the points whose distances from the two points are in that ratio. This turns out to be a circle.
1Other than . Picking the ratio gives the perpendicular bisector between the two points. Sometimes it's a useful point of view to think of lines as "circles through infinity".
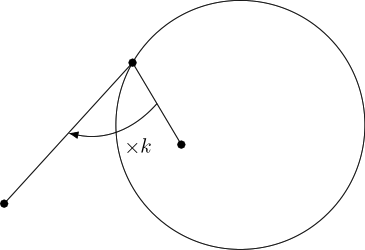
One way to think of this is to imagine two people standing at the two points. Suppose that one can run twice as fast as the other. Then the plane can be divided into two regions depending on which person can get there first. The boundary, consisting of those points that the two reach in the same time, is a circle.
For completeness, the complex number version is as follows. Let and with and , then the set of that satisfy the following condition is a circle,
While it's easy enough to show algebraically that this does describe a circle, that was never very satisfying. What I wanted was a geometric explanation. I've finally figured one out.
Unsurprisingly, it involves similar triangles yet again.
2 Algebra
The algebraic proof is straightforward. Let and be the coordinates of the points in the plane, let be the ratio of the distances. Let be a point such that the distance to is times its distance to .
Pythagoras' theorem says that the distance from to is:
and the distance from to is:
so the condition that the ratio is means that:
The square roots are annoying, so let's square both sides to get rid of them:
Expanding out the brackets leads to:
Gathering terms then gives:
which is obviously a circle.
Dividing2 by we get
2This is where we use the assumption that
Completing the square on both and leads to:
To deal with that mess on the right-hand side, we put it all over whereupon the numerator simplifies as follows:
and we recognise as the square of the distance between the two points and .
So the centre of the circle is at
and its radius is
3 Geometry
So, we know that it is a circle. But as a geometer, a purely algebraic method as above doesn't tell me why it is a circle. For that, I need to draw some pictures.
The first thing to see is that the description is coordinate free, and so we can scale, rotate, and translate it without changing the underlying geometry. This might have an effect on the constant, , but if we leave that free then that doesn't matter. So we can take our two points to be at the origin and at . The algebra then tells us that the centre is at:
and the radius is
Note that I'm using the algebra to inform my geometric investigation. I may be after a geometric reason, but I'm not going to ignore all the work I did on the algebra.
Let's now draw a picture. In the following, I'm going to tacitly assume that . If we had then we could swap the roles of and .
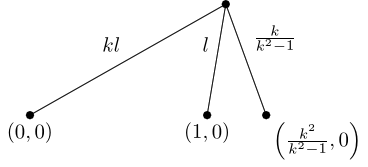
The denominator of is irritating, so let's scale everything up by that factor (we'll absorb it into as that's an arbitrary length).
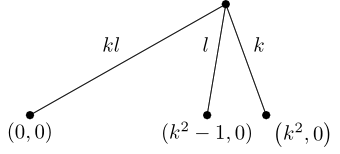
It will be a bit easier if we label lengths rather than coordinates, so we'll draw the line at the bottom and label the two lengths. Since the total distance is and the first part is then the second part now has distance . We'll label the points as well.
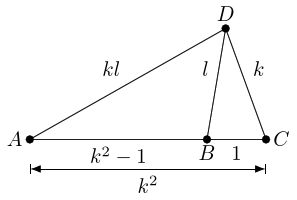
At this point, the answer leaps out. Triangle is similar to triangle with scale factor . As point moves, this similarity forces the relationship , which means that is constant as doesn't change. Hence, a circle.
Although we used the algebra to guide our drawing, the only part that still actually relies on the algebra is the location of the centre, . So to complete the geometric argument we need a geometric construction of .
Let's resume from the original diagram in which the distance between and was .
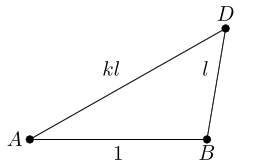
Knowing that similar triangles are the key, we note that the lengths and are defined by being in ratio , so the most natural thing to do is to place a triangle similar to with scale factor adjacent to . There are two ways round to do this and guided by what we know we'll choose the one so that the angle corresponding to ends up at .
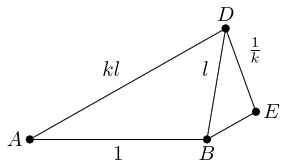
The length is , strongly suggesting that we do this again: place a similar triangle along .
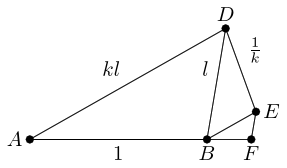
In this picture, and so we can continue the process along . But before we do so, let us note that because of how the triangles have been placed, and . Hence , , and between them comprise the three angles in the original triangle . Hence is a straight line.
The next step in the iteration adds a point on the continuation of the line , and the next on . As we have assumed that , the triangles are getting smaller (in a geometric series) and will therefore converge. Since we add successively points on the continuation lines through and through , the convergence point must be the intersection of these lines.
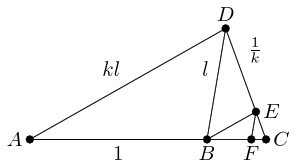
We can do more than that. The lengths that we add each time form a geometric series. We start with , then , then , and so on. Every other term adds to the continuation, and the in between terms to the continuation. Hence the intersection point is
from and
from . Neither of these depends on , and thus neither depends on where is providing it satisfies the criterion that .
Hence the locus of is a circle centred on , which lies on the line through at distance from , with radius .
4 Deep Mining the Geometry
The more I play with these pictures, the more geometry I find. Let's start with a triangle, with base length . We'll insist that it not be isosceles, and without loss of generality assume that the angle at is the larger of the base angles. As above, we'll look at the ratio of the two non-base sides, but this time we'll think of the ratio of the smaller to the larger.
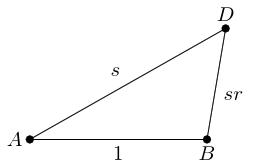
As before, we'll draw a line at angle to and mark where it meets the extension of .
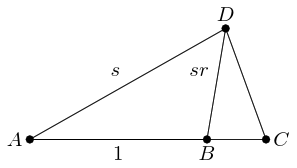
From the new point, , we draw a line parallel to and continue it to meet the extension of .
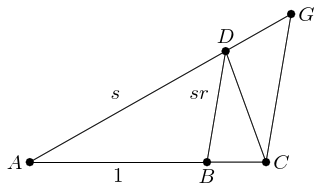
By construction, triangles and are similar. Therefore, angle . We also have that (by construction) and therefore (by alternate angles). Hence triangle is also similar to .
Looking at the angles, triangle is similar to .
We therefore have two basic triangles and all others are similar to one or other of these. Also, each triangle decomposes into two pieces which are similar to the two basic triangles. We can see this from the decomposition of into and , and of into and .
Continuing the decomposition on triangle and then on any copy of , we end up by filling by ever smaller copies of itself, establishing it as an irrep--tile. This decomposition coincides with the result of the earlier iteration.
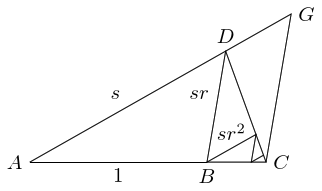
Here's an interactive version of that diagram, with added triangles showing the iteration going outwards as well as inwards. You can drag the vertices of the original triangle around.
What can also be seen from this is that the length of the zig-zag path, starting at and ending at , is the same as the direct path from to via . All the bits parallel to translate up to fill in the section , while all the bits parallel to , together with , translate to fill the section .
To find the size of the triangle , we use the various similarities. We have three similar triangles: , , and . As we have assumed that , the lengths of and define the scale factors. So if we put and then the triangles have the following lengths, where each column is a triangle and each row is a family of corresponding lengths:
Now appears twice in this table, so and thus . Also so and thus . Putting these together gives:
which rearranges to
and substituting back we get that
We've noted that is the same length as the zig-zag path, so:
which is a nice geometrical proof of the sum of a geometric series.
Getting back to the circle, we are expecting that the centre will be at so we need the position of and the distance to depend only on the ratio and not on . And this is exactly what we find since is on the line which passes through and at a distance from , and:
5 Animation
Lastly, here's an animation to demonstrate this topic. It shows what happens as the ratio varies. As with the previous animation, the points can be moved around.
