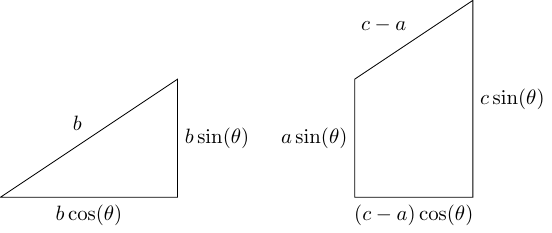1 Introduction

One of the classic applications of Pythagoras' theorem is to calculate the area of an annulus without measuring the radii of the two circles. In this post I want to look a bit more closely at why Pythagoras' theorem is relevant here beyond the simplistic "It just works".

As usual in my writings, my goal is always for me to understand something more deeply. In this case, I want to understand the interaction between Pythagoras' theorem and area. While I maintain that Pythagoras' theorem is about length, I can't deny its myriad applications to area – some of which can be used to prove Pythagoras' theorem. As the area of an annulus is such a classic, I wanted to examine it in more detail to see if I could understand just what Pythagoras' theorem had to do with it.

Doing this requires me working through the details for myself. I make no claim to originality, but I haven't gone looking for what others have done on similar lines because it is original to me and that's what counts.

2 Ingredients

In this post-Honey–π² era, I feel more than ever that I should lay out the ingredients for anything that I write so that a reader can truly see where the ideas came from. In that spirit, here are the raw ingredients for this one.

• A series of dissection proofs of Pythagoras' Theorem by Steve Phelps involving triangles, squares, pentagons, and hexagons.

  While I maintain that a true proof of Pythagoras' theorem should focus on length and not mention area, these are nevertheless fascinating animations. In looking at the sequence, I thought that if one made them so that the diameter of the shape was kept fixed rather than the side length then in the limit there would be a dissection of an annulus into a circle.

• A variety of puzzles (both old and new) by Catriona Shearer using the formula for the area of an annulus.

• A random picture posted by Ed Southall.

• And my current obsession with Pythagoras' theorem.

The formula for the area of an annulus is a classic in geometry. Catriona Shearer and I wrote about one of her puzzles based on it. It's a straightforward, and well-known, application of Pythagoras' theorem so it's never far from my mind when Pythagorean stuff is discussed. I found that Steve Phelps' dissection animations brought it to the fore due to the way that the smallest polygon was located in centre of the largest. This planted the idea for taking these dissections to the limit and seeing what they implied for the area of an annulus.

This idea lay dormant until Catriona Shearer posted a recent puzzle involving the area of an annulus (the one which we wrote about). As I wrote there, this linked in my mind with something I'd written on Pythagoras and the Intersecting Chords theorem. Writing that had also made me think about equivalents of Pythagoras' theorem, so this led me to look a bit more closely at the formula for the area of the annulus. Not necessarily with a view to using it to prove Pythagoras' theorem, but at least to try to understand what right-angled triangles had to do with it.

That last point is important. Take any shape and calculate its area, say $A$. Then there will be a (unique) circle whose area is $A$; the radius of this circle will be $\sqrt{\frac{A}{\pi }}$. So the fact that an annulus has the same area as a particular circle is not all that surprising. What is something of a shock is that the various radii can be put together into a triangle which has a right-angle.

3 First Dissection

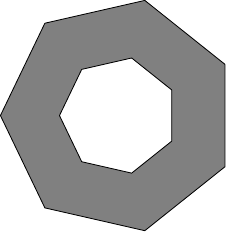
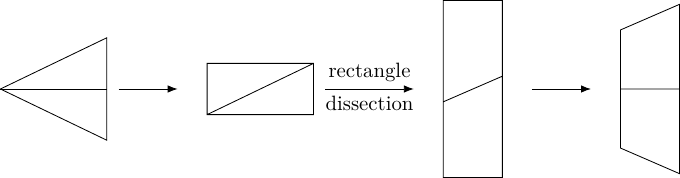
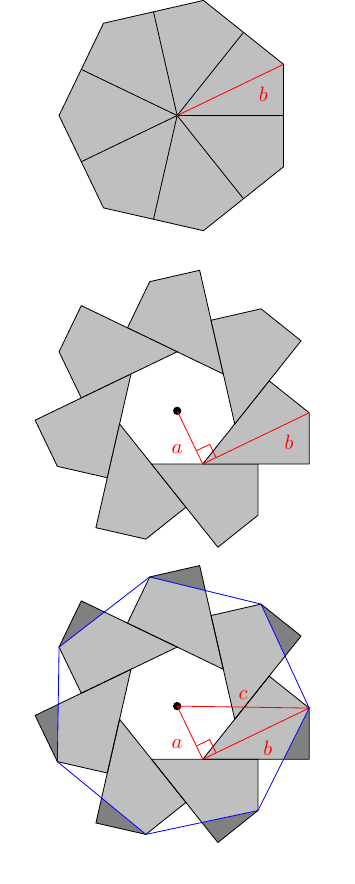
Although partially inspired by Steve Phelps' animations, I deliberately didn't re-examine them when looking at continuing the sequence. I therefore set out to consider the most obvious configuration. This is where the inner $n$–gon, of "radius" $a$, sits inside the larger $n$–gon, of "radius" $c$, in the most natural position, as in Figure 1.

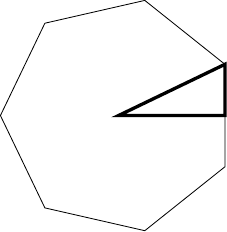
As my goal was to devise something that was independent of $n$, I quickly focussed on a small repeating unit: the right-angled triangles formed by bisecting each side, as in Figure 2.

This led to the problem of comparing a triangle with a trapezium, as in Figure 3. Here, $\theta =\frac{\pi }{n}$.

Starting from $c^2=a^2+b^2$, we can deduce that these two shapes have the same area and therefore each can be dissected and put together to form the other.

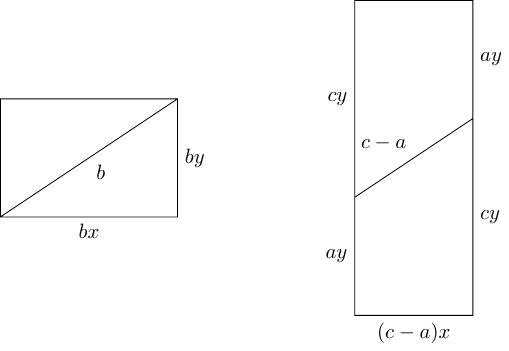
In true Honey–${\pi }^2$ fashion, I shall confess to making very little progress on this for some considerable time due to the fact that I was trying to match the sloping lines against each other and then trim the rest. I made more progress when I made each shape into a rectangle by doubling it up. Writing $x=\cos (\theta )$ and $y=\sin (\theta )$, the result is in Figure 4.

Knowing that $b^2=(c+a)(c-a)$ means that these two rectangles have the same area. I already know how to dissect rectangles that are the same area so I could simply apply that dissection. But I wasn't sure that that would behave well as the number of sides of the original polygon increased, so I tried a few others as well.

I did come up with what felt like a nicer dissection, which I will explain in a moment. Before I do so, though, I want to explain why it ended up as a dead end. Although I quite like it as a way of showing how to dissect a rectangle and reform it into another with the same area, there were two major issues.

The first was that I didn't want to dissect rectangles. I wanted to dissect a triangle and reform it into a trapezium. So no matter how simple my rectangle dissection (and in terms of number of cuts, it wasn't that simple), my overall process was guaranteed to feel complicated because it had to be preceded and postceded by more dissections, as in Figure 5.

The second was an issue with this whole approach which had been niggling at the back of my mind, but which I didn't confront until my unease with the complexity of this dissection forced me to consider it. This approach started with the fact that I had $a$, $b$, and $c$ satisfying $c^2=a^2+b^2$. That increasingly felt like the wrong starting place. As I said in the introduction, if we start with a polygonal annulus1 (as in Figure 1) with outer radius $c$ and inner radius $a$, then there is a $b$ (given by $\sqrt{c^2-a^2}$) such that the polygon with radius $b$ has the same area as that annulus. Having found $b$, we can apply some dissection regime to change the polygon into the annulus. But this doesn't feel as though it will lead to an explanation as to why the numbers $a$, $b$, and $c$ form a right-angled triangle.

With those provisos, let me explain the dissection method that I came up with. Although it was a dead end in this investigation, I still quite like it.

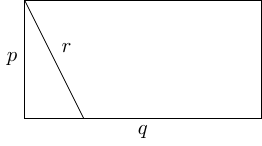
It starts with two rectangles of the same area. Let us suppose that the sides of the rectangles are $p,q$ and $r,s$, so that $pq=rs$. We can further assume that $p<r\le s<q$.

Draw the $pq$–rectangle in landscape orientation and then add a line of length $r$ starting from the top left corner and reaching the bottom edge2. This is illustrated in Figure 6.

The second step involves starting from this new point on the bottom edge and cutting at a right-angle to the sloped line. When this second line reaches either the top edge or the right-hand edge, it must be brought back on at the opposite edge. If the right-hand edge, it should be brought back on to the left-hand edge at the same height. If the top edge, it should be brought back on to the bottom edge at the point found by travelling parallel to the line of length $r$ (there is the possibility that this will be off the right-hand end of the bottom edge, in which case it wraps round). This line continues until it meets the line of length $r$.

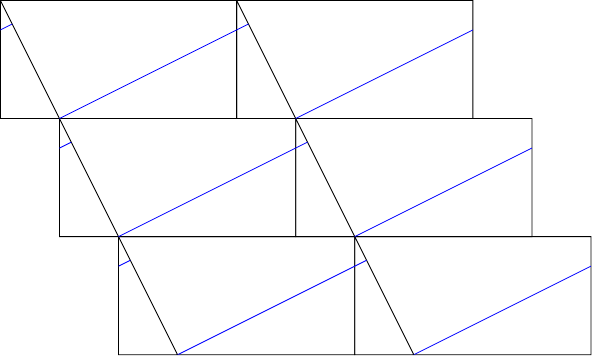
This may seem a little convoluted, and illustrating it would involve considering the various different cases, but there is a nice single picture that demonstrates all that is going on in which (in my view) makes it clear how the different possibilities are handled. This picture involves tessellation. Dissections and tessellations have a strong connection, as we will see in this case. We shall tessellate the rectangle from Figure 6 with a shift between rows such that the segments of length $r$ form a continuous line.

In Figure 7, the blue lines illustrate how the second cut works and the tessellation indicates how the pieces fit back together to form the second rectangle. The blue line has to be of length $s$ because the areas of the two rectangles are the same.

The tessellation picture also shows, I think, that the choice of insisting that we start with $p$, $q$, $r$ satisfying $p<r<q$ was one that can be discarded. Indeed, I feel that there is much scope for exploration with this picture if one has not encountered it before. But that is outside the scope of this article so, given the drawbacks with this approach that I identified earlier, I will leave this here.

4 Second Dissection

As I said at the start of the previous section, I slightly deliberately didn't look back at Steve Phelps' original animations (the "slightly" is because it would also have been a bit of a bother since searching for an animation on twitter – which is where I first saw them – is not the easiest of tasks). But one thing that lingered from my initial encounter with them was that although the dissection had $n$–fold symmetry, it didn't start by nicely splitting the polygon into the triangle/trapezium pieces as my previous approach had been trying.

This is where a chance picture from Ed Southall happened to strike the inspiration node in my brain3. That gave me the idea that the pieces of the annulus might get twisted as they get put back together into the polygon.

Although I'm trying to be true to the spirit of Honey–${\pi }^2$ here, I shan't detail every blind alley I stumbled down on this part. None of them got to quite as nice a destination (albeit a wrong 'un) as the alley in Section 3 and I didn't explore them as much. Suffice it to say that it took me a while to overcome the seductive fact that both the solid $n$–gon and the $n$–gon annulus had lots of angles in common so it was natural to try to match them up. The problem with this approach was that while the angles match, the side lengths have no nice relationship4. So in trying to match the angles, the sides would be messy.

I also had a second, more minor, misconception which was that when splitting up the solid $n$–gon then I would start by splitting it into isosceles triangles, as in the starting point of Figure 5.

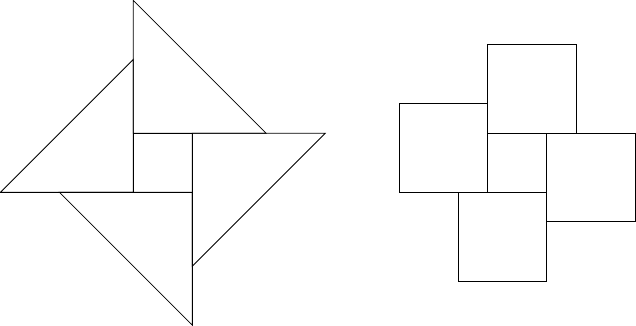
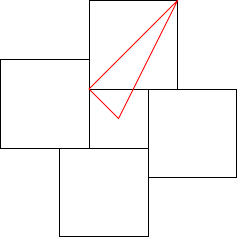
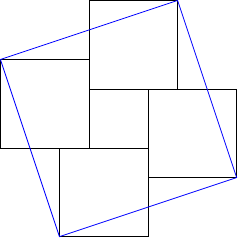
What shook me out of both of these misconceptions was looking at a very simple case: squares. I wanted to start with a square of size5 $b$, dissect it, and put the pieces around a square of size $a$ to create a square of size $c$. The two pictures I found myself considering were the two in Figure 8.

Neither of these makes a square, but both can be further "pruned and grafted" to make one. The "Aha!" moment came when I put in lines to indicate the sizes of the squares. In the right-hand picture, after the "pruning and grafting" step, the corners of the largest square (of size $c$) coincide with certain corners of the surrounding squares. Joining these to the corners of the square of size $a$ amounts to drawing in the diagonals of the surrounding squares. But because these surrounding squares are actually parts of the square of size $b$, these diagonals translate to the (maxiumum) radius of the square of size $b$ (which could be called the semi-diagonal). Drawing in all of these led to the "Aha!". I'll put in Figure 9 now to let you see if you can see it.

There was a second, but smaller, "Aha!" which came when I joined up the corners of the outermost square and realised that the "pruning and grafting" step was obvious. The point here being that in both of the pictures in Figure 8 then I knew it was possible to trim the excesses and fill in the deficiencies to make a square of the required size, but with the left-hand one I had to do some calculations to decide where to make the cuts and this felt perilously close to solving the problem by knowing the answer beforehand. On the right-hand picture, however, Figure 10 shows that the excess that needs to be trimmed is obvious and equally obviously fills in the deficiency. Therefore I don't need to know in advance that the outermost square is of size $c$, it becomes so by construction.

So the full process is as follows.

1. Fix $n$–gons whose major radii are $a$ and $b$.

2. Dissect the size $b$ $n$–gon into congruent kites by joining the midpoint of each side to the centre.

   Note that the equal angles in these kites are right-angles.

3. Place each kite along an edge of the size $a$ $n$–gon so that the point which was at the centre of the size $b$ $n$–gon is at a vertex of the size $a$ $n$–gon.

4. Join up the vertices of the size $b$ $n$–gon in their current location.

5. Cut off the protruding triangles and use each to fill in its neighbouring intruding triangle.

   Note that each of these triangles is a right-angled triangle whose sides are half the sides of the various $n$–gons.

6. The result is an $n$–gon of size $c$, where $a$, $b$, $c$ forms a right-angled triangle.

   That right-angled triangle can be seen by joining the centre to a vertex of $a$, then to the corresponding vertex of the $c$, and back to the centre.

   Also worth noting somewhere is that in the $n$–gon annulus, the two $n$–gons are (possibly) rotationally offset from each other.

The right-angle is evident. The dissection shows that the area of the annulus $n$–gon is equal to the area of the original $n$–gon. Each area is a fixed multiple of the square of its size, thus demonstrating that:

$$c^2-a^2=b^2$$

I bet you weren't expecting that!

5 Proof by General Picture

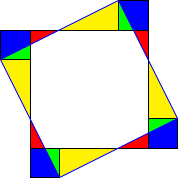
This isn't quite "proof by picture", but a lot of the argument is contained within the pictures of Figure 11 and in any such proof or construction it is important to check that the picture conveys the whole story.

In this case, there are some edge cases. Because the inner polygon in the annulus is twisted with respect to the outer one, it is possible that the vertices of the inner polygon project outside the vertices of the outer one (even with $c>a$). For a given $a$ and $b$, there is an upper bound on $n$ where this occurs.

Note that a necessary condition for this to happen is that the kites not stretch far enough along the sides of the inner polygon, but this is not sufficient. An exact condition requires a little trigonometry and will be given at the end of this section.

An example of this edge case is given in Figure 12. The annulus area in this case is the difference of the areas of the two polygons, which means that the red areas should be counted negatively as they are inside the inner polygon but outside the outer one. Thus in Figure 12, the area we wish to calculate is the yellow plus the green minus the red. The goal is to show that this is equal to the blue plus the green.

With the obvious abbreviations, we need to show that:

$$Y+G-R=B+G$$

This simplifies to $Y=B+R$, which is the generalisation of the dissection method.

Let us conclude this section with the condition under which this edge case occurs. Let $\varphi$ be the angle at the origin in the $a$–$b$–$c$ triangle (so $a\tan (\varphi )=b$). Let $\theta =\frac{\pi }{n}$ be half the angle at the centre of the polygon. Let $k$ be such that $2k\theta \le \varphi <2(k+1)\theta$ and put $\alpha =\varphi -2k\theta$. This is the angle between a vertex of the inner polygon and the next vertex anticlockwise of the outer polygon. Then the condition for this edge case to occur is:

$$\frac{\cos (\theta )}{\cos (\alpha -\theta )}<\frac{a}{c}.$$

6 Conclusion

If I were to extract some general principles on "doing Mathematics" from this post they would be the following:

1. Explore alleyways, be prepared for them to lead somewhere interesting but not necessarily useful to what you're trying to do.

   That sense of "there's got to be an easier way" is something that develops as one practises doing maths.

2. When trying an idea, don't hold the pieces too tightly. Allow room for manoeuvre, don't get fixated on a detail in your argument but give yourself permission to change your mind.

   (Having said that, keep careful notes! It's important that you are consistent with your changes so that you don't have half the construction relying on $x$ being this length and half on it being that one.)

3. Let things stew. If you find yourself getting stuck, take a break. Keep it nearby in case inspiration strikes, but allow yourself to work on something else for a bit.

4. Look for help or inspiration on your own terms. I decided early on not to look at similar writings, and not to look back at Steve Phelps' animations6. This was because I was fairly confident I would be able to "do the math" and my goal was to understand things more deeply, which I do by working through them myself. However, I've been working through Pythagorean ideas for some time now and so have a reasonable sense of what I'm capable of.

   6In retrospect, this was a Very Good Idea else I would have discovered this dissection which is so close to what I've ended up with that had I seen that I would probably have just not bothered. The key difference is the placement of the right-angled triangle and that I use the radius rather than the side length in that triangle.

As for this particular journey, I feel I now have a clearer picture of why the area of an annulus is the area of a particular circle. I can imagine cutting the circle into tiny kites and laying these kites around the annulus, each tangential to the inner circle. Then of course the length of the kite is equal to the half-length of the tangential chord. But it is the laying tangentially that is crucial here, and this is why right-angles enter the picture.

As a bonus, we get an infinite number of dissection proofs of Pythagoras' theorem!

This actually answers a question posed on Cut the Knot:

The applet [on that page] illustrates a thought experiment. In two concentric circles of radii $a$ and $c$, ($a<c$), the semitangent to the small circle contained by the big circle is allowed to rotate. The semitangent of length $b$, sweeps an area which after a complete turn covers the ring between the two circles. The area of the ring is $\pi (c^2-a^2)$. Were it possible to find a proof independent of the Pythagorean theorem that the area swept by the $b$ segment is indeed $\pi b^2$, we would get an additional proof of the Pythagorean theorem itself.

The crucial fact in the thought experiment is that the sweeping line shouldn't be thought of as being a line of constant thickness. Similarly, when a rotating line sweeps out a circle, that line also shouldn't be thought of as being of constant thickness. The connection is that both get "thicker" by just the right amount. As everything here is infinitesimal, we make this precise by using regular polygons and then letting the number of sides tend to infinity.

To finish, here's a geogebra applet that you can use to play around with this construction.